题目内容
已知有序实数对(a,b)满足a∈[O,3],b∈[0,2],则关于x的一元二次方程x2+2ax+b2=0有实数根的概率是 .
【答案】分析:本题考查的知识点是几何概型的意义,关键是要找出(a,b)对应图形的面积,及满足条件“关于x的一元二次方程x2+2ax+b2=0有实根”的点对应的图形的面积,然后再结合几何概型的计算公式进行求解.
解答: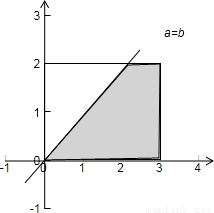 解:如下图所示:试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}(图中矩形所示).
解:如下图所示:试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}(图中矩形所示).
其面积为6.
而构成事件“关于x的一元二次方程x2+2ax+b2=0有实根”的区域为
{(a,b)|0≤a≤3,0≤b≤2,a≥b}(如图阴影所示).
所以所求的概率为=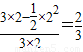 .
.
故选B
点评:本题考查的知识点是几何概型的意义,关键是要找出关于x的一元二次方程x2+2ax+b2=0有实根”的点对应的图形的面积,并将其和长方形面积一齐代入几何概型计算公式进行求解.
解答:
 解:如下图所示:试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}(图中矩形所示).
解:如下图所示:试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}(图中矩形所示).其面积为6.
而构成事件“关于x的一元二次方程x2+2ax+b2=0有实根”的区域为
{(a,b)|0≤a≤3,0≤b≤2,a≥b}(如图阴影所示).
所以所求的概率为=
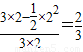 .
.故选B
点评:本题考查的知识点是几何概型的意义,关键是要找出关于x的一元二次方程x2+2ax+b2=0有实根”的点对应的图形的面积,并将其和长方形面积一齐代入几何概型计算公式进行求解.

练习册系列答案
相关题目