题目内容
设直线l:4x+3y+a=0和圆C:x2+y2+2x-4y=0.(1)当直线l过圆C的圆心时,求实数a的值;
(2)当a=3时,求直线l被圆C所截得的弦长.
【答案】分析:(1)求出圆C的圆心为(-1,2),代入直线l方程并解之即可得到实数a值.
(2)设直线l与圆C交于M、N两点,作CD⊥l于D点.利用点到直线的距离公式算出C到l的距离,再由垂径定理即可算出直线l被圆C所截得的弦长.
解答:解:(1)由x2+y2+2x-4y=0,化成标准方程得(x+1)2+(y-2)2=5.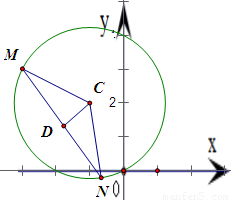
∴圆C的圆心为(-1,2),半径r=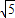 . …(2分)
. …(2分)
∵直线l过圆C(-1,2),
∴C的坐标代入,得-4+6+a=0,解得a=-2. …(4分)
(2)设直线l与圆C交于M、N两点,作CD⊥l于D点
当a=3时,圆心(-1,2)到直线l:4x+3y+3=0的距离为
d=|CD|=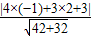 =1. …(7分)
=1. …(7分)
因此,可得|MN|=2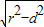 =2
=2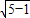 =4.
=4.
即直线l被圆C所截得的弦长为4. …(10分)
点评:本题给出已知圆和动直线,求当直线l过圆时的a值,并求直线l被圆截得的弦长.着重考查了圆的方程、点到直线的距离公式和垂径定理等知识,属于中档题.
(2)设直线l与圆C交于M、N两点,作CD⊥l于D点.利用点到直线的距离公式算出C到l的距离,再由垂径定理即可算出直线l被圆C所截得的弦长.
解答:解:(1)由x2+y2+2x-4y=0,化成标准方程得(x+1)2+(y-2)2=5.

∴圆C的圆心为(-1,2),半径r=
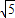 . …(2分)
. …(2分)∵直线l过圆C(-1,2),
∴C的坐标代入,得-4+6+a=0,解得a=-2. …(4分)
(2)设直线l与圆C交于M、N两点,作CD⊥l于D点
当a=3时,圆心(-1,2)到直线l:4x+3y+3=0的距离为
d=|CD|=
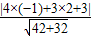 =1. …(7分)
=1. …(7分)因此,可得|MN|=2
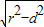 =2
=2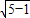 =4.
=4.即直线l被圆C所截得的弦长为4. …(10分)
点评:本题给出已知圆和动直线,求当直线l过圆时的a值,并求直线l被圆截得的弦长.着重考查了圆的方程、点到直线的距离公式和垂径定理等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目