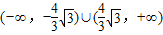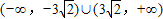题目内容
已知圆C:x2-2x+y2-2=0,点A(-2,0)及点B(4,a),从A点观察B点,要使视线不被圆C挡住,则实数a的取值范围是( )A.(-∞,-1)∪(1,+∞)
B.(-∞,-2)∪(2,+∞)
C.
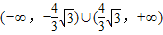
D.
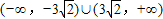
【答案】分析:先设过A的直线方程为:kx-y+2k=0,根据“使视线不被圆C挡住”则找到直线与圆相切的位置,这样,先求得圆心到直线的距离,再让其等于半径,求得切线方程,再令x=4得
y=±3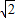 ,从而求得实数a的取值范围.
,从而求得实数a的取值范围.
解答: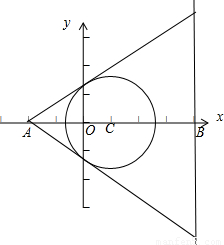 解:圆C:x2-2x+y2-2=0 即(x-1)2+y2=3.
解:圆C:x2-2x+y2-2=0 即(x-1)2+y2=3.
设过A的直线方程为:kx-y+2k=0,圆心(1,0)到直线的距离为:d=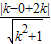 .
.
∵直线与圆相切,∴d=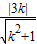 =r=
=r=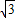 ,解得k=±
,解得k=±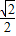 .
.
故圆的过点A(-2,0)的切线方程为 y=±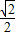 (x+2).
(x+2).
再把x=4代入圆的切线方程求得y=±3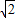 ,
,
故要使视线不被圆C挡住,则实数a的取值范围是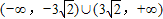 ,
,
故选D.
点评:本题主要考查直线与圆的位置关系,作为相切是研究相交和相离的关键位置,应熟练掌握,属于中档题.
y=±3
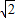 ,从而求得实数a的取值范围.
,从而求得实数a的取值范围.解答:
 解:圆C:x2-2x+y2-2=0 即(x-1)2+y2=3.
解:圆C:x2-2x+y2-2=0 即(x-1)2+y2=3.设过A的直线方程为:kx-y+2k=0,圆心(1,0)到直线的距离为:d=
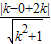 .
.∵直线与圆相切,∴d=
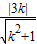 =r=
=r=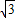 ,解得k=±
,解得k=±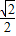 .
.故圆的过点A(-2,0)的切线方程为 y=±
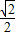 (x+2).
(x+2).再把x=4代入圆的切线方程求得y=±3
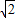 ,
,故要使视线不被圆C挡住,则实数a的取值范围是
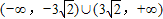 ,
,故选D.
点评:本题主要考查直线与圆的位置关系,作为相切是研究相交和相离的关键位置,应熟练掌握,属于中档题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目