题目内容
若实数x, y满足x2+y2-2x+4y=0,则x-2y的最大值是( )
A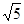 B10 C9 D5+2
B10 C9 D5+2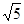
A
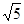 B10 C9 D5+2
B10 C9 D5+2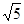
B
先根据约束条件画出图形,设z=x-2y,再利用z的几何意义求最值,只需求出直线z=x-2y过图形上的点B时,从而得到z=x-2y的最大值即可.
解答:解:先根据x,y满足x2+y2-2x+4y=0画出图形,

设z=x-2y,
将z的值转化为直线z=x-2y在y轴上的截距,
当直线z=x-2y经过点A(2,-4)时,z最大,
最大值为:10.
故x-2y的最大值为10.
解答:解:先根据x,y满足x2+y2-2x+4y=0画出图形,

设z=x-2y,
将z的值转化为直线z=x-2y在y轴上的截距,
当直线z=x-2y经过点A(2,-4)时,z最大,
最大值为:10.
故x-2y的最大值为10.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
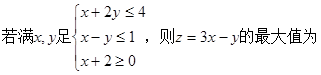 .
. 满足
满足 则
则 的最小值为( )
的最小值为( )



 的最大值为
的最大值为 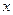 、
、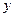 ,满足
,满足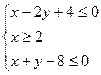 ,则
,则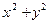 的取值范围为( )
的取值范围为( )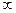 ,13]
,13]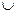 [40,+
[40,+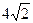 ]
]
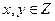 ,
,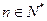 ,设
,设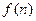 是不等式组
是不等式组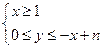 ,表示的平面区域内可行解的个数,
,表示的平面区域内可行解的个数, 由此
由此 可推出
可推出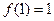 ,
, ,……, 则
,……, 则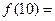 ( )
( )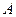 为不等式组
为不等式组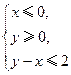 表示的平面区域,则
表示的平面区域,则 从-2连续变
从-2连续变 化到1时,动直线
化到1时,动直线 扫过
扫过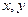 满足约束条件
满足约束条件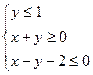 ,则
,则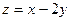 的最大值为_________.
的最大值为_________.