题目内容
若a，b，c均为正实数，则三个数a+
，b+
，c+
（ ）
| 1 |
| b |
| 1 |
| a |
| 1 |
| a |
分析：根据基本不等式，利用反证法思想，可以确定a+
，b+
至少有一个不小于2，从而可以得结论．
| 1 |
| b |
| 1 |
| a |
解答：解：由题意，∵a，b均为正实数，
∴a+
+b+
≥ 4
当且仅当a=b时，取“=”号
若a+
＜2，b+
＜2，则结论不成立，
∴a+
，b+
，至少有一个不小于2
∴a+
，b+
，c+
至少有一个不小于2
故选D．
∴a+
| 1 |
| b |
| 1 |
| a |
当且仅当a=b时，取“=”号
若a+
| 1 |
| b |
| 1 |
| a |
∴a+
| 1 |
| b |
| 1 |
| a |
∴a+
| 1 |
| b |
| 1 |
| a |
| 1 |
| a |
故选D．
点评：本题的考点是不等式的大小比较，考查基本不等式的运用，考查了反证法思想，难度不大
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
（2009•普陀区一模）如图，已知圆C：x2+y2=r2与x轴负半轴的交点为A．由点A出发的射线l的斜率为k，且k为有理数．射线l与圆C相交于另一点B．
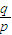，其中p、q均为整数且p、q互质）
，其中p、q均为整数且p、q互质）