题目内容
设a、b是方程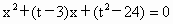 的两个实根,并已知函数
的两个实根,并已知函数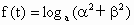 .
.
(1)求函数f(t)的解析式与定义域;
(2)讨论函数f(t)的单调性;
(3)当a=2时,求f(t)在定义域上的最大值与最小值.
答案:略
解析:
提示:
解析:
|
根据二次方程判别式求出 t的范围,然后由韦达定理求出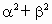 的表达式. 的表达式.
解: (1)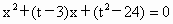 有实根,则 有实根,则
又 ∴ (2)设 ∴当a>1时,f(t)在[-7,-3)上单调递增。在[-3,5)上单调递减; 当0<a<1时,f(t)在[-7,-3]上单调递减,在[-3,5)上单调递增. (3)当a=2时, |
提示:
|
复合函数单调性取决于减函数的个数,如果减函数为偶数个,则原函数为增函数,如果减函数为奇数个,则原函数为减函数. |

练习册系列答案
相关题目
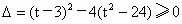 ,解得-7≤t≤5.
,解得-7≤t≤5.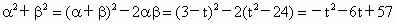 ,
,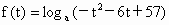 ,tÎ
[-7,5].
,tÎ
[-7,5].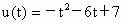 ,对称轴为t=-3,
,对称轴为t=-3,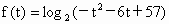 最大值为
最大值为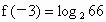 ,最小值为f(5)=1.
,最小值为f(5)=1.