题目内容
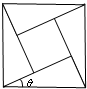2002年8月，在北京召开国际数学家大会，大会会标如图所示，它是由四个相同的直角三角形、与中间的小正方形拼成的大正方形．若直角三角形中较小的锐角为θ，大正方形的面积为1，小正方形的面积为| 1 |
| 25 |
| 7 |
| 5 |
| 7 |
| 5 |
分析：根据正方形的面积=边长2，可知大正方形及小正方形的边长，根据图形，大正方形的边长即是直角三角形的斜边，小正方形的边长即是直角三角形两个直角边的差，从而可求相应三角函数的值．．
解答：解：由题意，大正方形的边长为1，小正方形的边长为
设θ所对的直角边为x，则由勾股定理得：x2+(x+
)2=1
∴x=
，∴sinθ=
，cosθ=
∴sinθ+cosθ=
故答案为：
| 1 |
| 5 |
设θ所对的直角边为x，则由勾股定理得：x2+(x+
| 1 |
| 5 |
∴x=
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∴sinθ+cosθ=
| 7 |
| 5 |
故答案为：
| 7 |
| 5 |
点评：本题的考点是在实际问题中建立三角函数模型，主要考查求解三角函数，关键是理解题意，正确利用勾股定理
练习册系列答案
阅读快车系列答案
相关题目
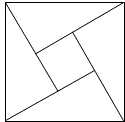2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是1，小正方形的面积是
2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小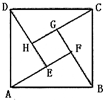
2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较大的锐角为θ，大正方形的面积是1，小正方形的面积是
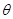，大正方形的面积是1，小正方形的面积是
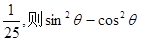的值等于（ ）
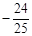C．
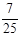D．