题目内容
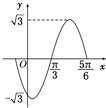 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π),x∈R的部分图象,则下列命题中,正确命题的序号为
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π),x∈R的部分图象,则下列命题中,正确命题的序号为
①函数f(x)的最小正周期为
| π |
| 2 |
②函数f(x)的振幅为2
| 3 |
③函数f(x)的一条对称轴方程为x=
| 7π |
| 12 |
④函数f(x)的单调递增区间为[
| π |
| 12 |
| 7π |
| 12 |
⑤函数的解析式为f(x)=
| 3 |
| 2π |
| 3 |
分析:通过函数的图象,求出T,求出ω,然后求出A,判断①②的正误;利用x=
=
,判断③的正误;利用函数的单调性判断④的正误;通过特殊点求出φ,判断⑤的正误即可.
| ||||
| 2 |
| 7π |
| 12 |
解答:解:由图象可知,函数f(x)的最小正周期为(
-
)×2=π,故①不正确;
函数f(x)的振幅为
,故②不正确;
函数f(x)的一条对称轴方程为x=
=
,故③正确;
④不全面,函数f(x)的单调递增区间应为[
+2kπ,
+2kπ],k∈Z;
⑤由
sin(2×
+φ)=
得2×
+φ=
+2kπ,k∈Z,即φ=2kπ-
,k∈Z,∵-π<φ<π,故k取0,从而φ=-
,故f(x)=
sin(2x-
).
故答案为:③⑤
| 5π |
| 6 |
| π |
| 3 |
函数f(x)的振幅为
| 3 |
函数f(x)的一条对称轴方程为x=
| ||||
| 2 |
| 7π |
| 12 |

④不全面,函数f(x)的单调递增区间应为[
| π |
| 12 |
| 7π |
| 12 |
⑤由
| 3 |
| 7π |
| 12 |
| 3 |
| 7π |
| 12 |
| π |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
故答案为:③⑤
点评:本题是基础题,考查三角函数的图象,求解函数的解析式的方法,函数的基本性质的应用,考查计算能力,逻辑推理能力,是常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象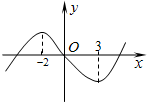 如图是函数f(x)=x3+bx2+cx+d图象,则函数y=x2+2bx+c的单调递增区间为( )
如图是函数f(x)=x3+bx2+cx+d图象,则函数y=x2+2bx+c的单调递增区间为( )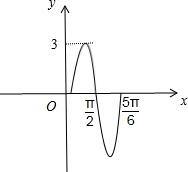 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤ (2013•温州二模)若如图是函数f(x)=sin2x和函数g(x)的部分图象,则函数g(x)的解析式可能是( )
(2013•温州二模)若如图是函数f(x)=sin2x和函数g(x)的部分图象,则函数g(x)的解析式可能是( )