题目内容
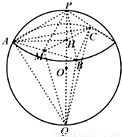
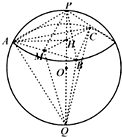 如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是
如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是4
4
.分析:取AB的中点M,连接PM,QM,则PM⊥AB,CM⊥AB,QM⊥AB,故∠PMC是侧面PAB与底面所成二面角的平面角,∠QMC是侧面QAB与底面所成二面角的平面角,由此可得结论.
解答:解:如图,取AB的中点M,连接PM,QM,则PM⊥AB,CM⊥AB,QM⊥AB
∴∠PMC是侧面PAB与底面所成二面角的平面角,∠QMC是侧面QAB与底面所成二面角的平面角,
∴∠PMC=45°,
设PR=h,OP=R,则MR=h,OR=R-h,
∴R2=4h2+(R-h)2,
∴R=2.5h
∴QR=4h
∵MR=h
∴正三棱锥Q-ABC的侧面与底面所成角的正切值是
=4
故答案为:4.

∴∠PMC是侧面PAB与底面所成二面角的平面角,∠QMC是侧面QAB与底面所成二面角的平面角,
∴∠PMC=45°,
设PR=h,OP=R,则MR=h,OR=R-h,
∴R2=4h2+(R-h)2,
∴R=2.5h
∴QR=4h
∵MR=h
∴正三棱锥Q-ABC的侧面与底面所成角的正切值是
| QR |
| MR |
故答案为:4.
点评:本题考查面面角,考查学生的计算能力,正确作出面面角是关键,属于中档题.

练习册系列答案
相关题目
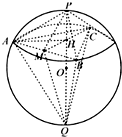 如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是________.
如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是________.