题目内容
下列四个命题:
①使用抽签法,每个个体被抽中的机会相等;
②利用秦九韶算法
,求多项式 f(x)=x5+2x3-x2+3x+1在x=1的值时v3=2;
③“-3<m<5”是“方程
+
=1表示椭圆”的必要不充分条件;
④?a∈R,对?x∈R,使得x2+2x+a<0
其中真命题为
①使用抽签法,每个个体被抽中的机会相等;
②利用秦九韶算法
|
③“-3<m<5”是“方程
| x2 |
| 5-m |
| y2 |
| m+3 |
④?a∈R,对?x∈R,使得x2+2x+a<0
其中真命题为
①②③
①②③
(填上序号)分析:①根据抽样的定义和性质判断.②根据秦九韶算法进行判断.③利用充分条件和必要条件的定义进行判断.④根据含有量词的命题的定义进行判断.
解答:解:①根据抽样的定义可知,任何抽样都必须保证抽出的公平性,即每个个体被抽中的机会相等,∴①正确.
②f(x)=x5+2x3-x2+3x+1=((((x+0)x+2)x-1)x+3)x+1
∴v3=((x+0)x+2)x-1
将x=1代入得v3=((1+0)×1+2)×1-1=3-1=2.∴②正确.
③当m=1时,方程为
+
=1,此时方程表示为圆,若方程
+
=1表示椭圆,
则
,即
,∴-3<m<5且m≠1,
∴“-3<m<5”是“方程
+
=1表示椭圆”的必要不充分条件,∴③正确.
④∵二次函数y=x2+2x+a,开口向上,∴?x∈R,使得x2+2x+a<0不成立,∴④错误.
故正确的是①②③.
故答案为:①②③.
②f(x)=x5+2x3-x2+3x+1=((((x+0)x+2)x-1)x+3)x+1
∴v3=((x+0)x+2)x-1
将x=1代入得v3=((1+0)×1+2)×1-1=3-1=2.∴②正确.
③当m=1时,方程为
| x2 |
| 4 |
| y2 |
| 4 |
| x2 |
| 5-m |
| y2 |
| m+3 |
则
|
|
∴“-3<m<5”是“方程
| x2 |
| 5-m |
| y2 |
| m+3 |
④∵二次函数y=x2+2x+a,开口向上,∴?x∈R,使得x2+2x+a<0不成立,∴④错误.
故正确的是①②③.
故答案为:①②③.
点评:本题主要考查命题的真假判断,涉及的知识点较多,要求熟练掌握相应的知识.

练习册系列答案
相关题目

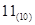 化为二进制数为
化为二进制数为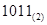 ;
;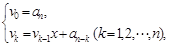
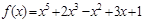 在
在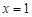 的值时
的值时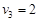 ;
;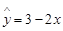 ,则变量
,则变量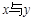 之间具有正相关关系.
之间具有正相关关系. 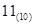 化为二进制数为
化为二进制数为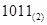 ;
;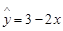 ,则变量
,则变量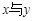 之间具有正相关关系;
之间具有正相关关系;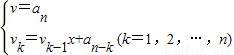 求多项式 f(x)=x5+2x3-x2+3x+1在x=1的值时v3=2;
求多项式 f(x)=x5+2x3-x2+3x+1在x=1的值时v3=2;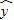 =3-2x,则变量x与y之间具有正相关关系.
=3-2x,则变量x与y之间具有正相关关系.