题目内容
在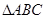 中,
中,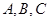 的对边分别是
的对边分别是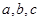 ,已知
,已知 .
.
(1)求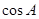 的值;
的值;
(2)若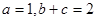 求
求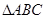 的面积
的面积
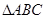 中,
中,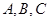 的对边分别是
的对边分别是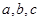 ,已知
,已知 .
.(1)求
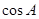 的值;
的值;(2)若
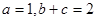 求
求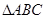 的面积
的面积(1)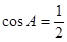 (2)
(2)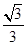
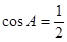 (2)
(2)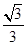
(1)因为 ,所以由正弦定理可转化为
,所以由正弦定理可转化为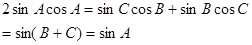
从而求出cosA.
(2)在(1)的基础上可求出sinA,所以求面积关键是求出bc,
然后利用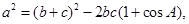 可求出bc,进而利用公式
可求出bc,进而利用公式 求值即可.
求值即可.
解:(1)法一:由已知 及正弦定理
及正弦定理
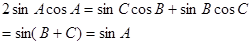
所以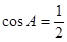 ………6分
………6分
法二:由余弦定理
有c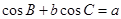 ,代入已知条件得
,代入已知条件得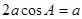
所以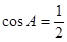
(2)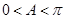 , 由
, 由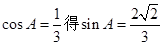 ,
,
由已知a=1,b+c=2
据余弦定理: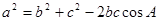 得1=
得1=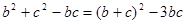
所以bc=1
所以三角形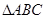 的面积S=
的面积S=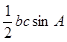 =
=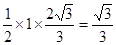 ………12分
………12分
 ,所以由正弦定理可转化为
,所以由正弦定理可转化为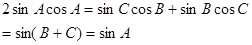
从而求出cosA.
(2)在(1)的基础上可求出sinA,所以求面积关键是求出bc,
然后利用
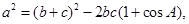 可求出bc,进而利用公式
可求出bc,进而利用公式 求值即可.
求值即可.解:(1)法一:由已知
 及正弦定理
及正弦定理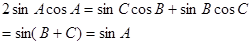
所以
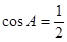 ………6分
………6分法二:由余弦定理

有c
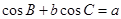 ,代入已知条件得
,代入已知条件得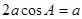
所以
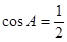
(2)
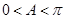 , 由
, 由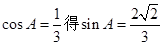 ,
,由已知a=1,b+c=2
据余弦定理:
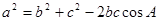 得1=
得1=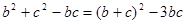
所以bc=1
所以三角形
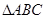 的面积S=
的面积S=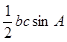 =
=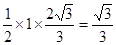 ………12分
………12分
练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
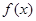 的定义域;(2)设
的定义域;(2)设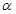 是第二象限的角,且tan
是第二象限的角,且tan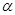 =
=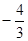 ,求
,求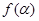 的值.
的值.  、
、 为锐角,且
为锐角,且 ,
, ,求
,求 的值.
的值.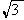 (tanA-tanB)=1+tanA·tanB.
(tanA-tanB)=1+tanA·tanB.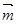 =(sinA,cosA),
=(sinA,cosA),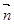 =(cosB,sinB),求|3
=(cosB,sinB),求|3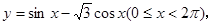 取最大值时,
取最大值时, 。
。
 )-sin
)-sin =
=  ,则sin(
,则sin( -
- )的值是( )
)的值是( )
 ,则
,则 的值为 ;
的值为 ;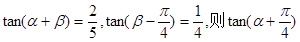 的值是。
的值是。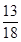
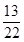
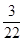
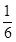
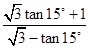 的值是
的值是