题目内容
(1)已知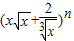 展开式中前3项系数的和为129,这个展开式中是否含有常数项和一次项?如果没有,请说明理由;如有,请求出来.
展开式中前3项系数的和为129,这个展开式中是否含有常数项和一次项?如果没有,请说明理由;如有,请求出来.(2)设
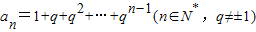 ,
,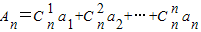
①用q和n表示An;
②求证:当q充分接近于1时,
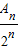 充分接近于
充分接近于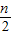 .
.
【答案】分析:(1)先求得展开式的通项公式,根据展开式中前3项系数的和为129,求得n的值,令x的幂指数等于零,自然数r无解,可得展开式中无常数项.令x的幂指数等于1,解得自然数r=6,由此可得展开式的一次项.
(2)①先求得 an=1+q+q2+…+qn-1= ,可得An =
,可得An =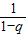 [(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)],再利用二项式系数的性质化简为
[(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)],再利用二项式系数的性质化简为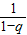 [2n-(1+q)n].
[2n-(1+q)n].
②由①求得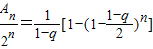 ,当q充分接近于1时,
,当q充分接近于1时,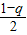 接近于0,由二项式定理知
接近于0,由二项式定理知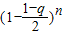 充分接近于
充分接近于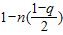 ,可得
,可得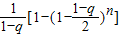 充分接近
充分接近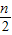 ,命题得证.
,命题得证.
解答:解:(1)二项式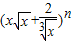 的展开式的通项公式为 Tr+1=
的展开式的通项公式为 Tr+1=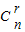 •
•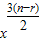 •2r•
•2r•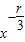 =
=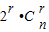 •
•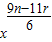 ,
,
展开式中前3项系数的和为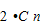 +
+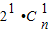 +
+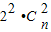 =129,解得n=8.
=129,解得n=8.
故通项公式为 Tr+1=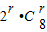 •
•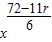 ,令
,令 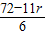 =0,自然数r无解,故展开式中没有常数项.
=0,自然数r无解,故展开式中没有常数项.
令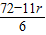 =1,解得自然数r=6,故有一次项,且一次项为1792x.
=1,解得自然数r=6,故有一次项,且一次项为1792x.
(2)①因为q≠1,所以,an=1+q+q2+…+qn-1=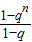 .
.
于是,An=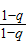
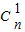 +
+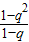
 +…+
+…+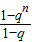 Cnn =
Cnn =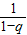 [(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]
[(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]
=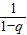 {(2n-1)-[(1+q)n-1]}=
{(2n-1)-[(1+q)n-1]}=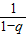 [2n-(1+q)n].
[2n-(1+q)n].
②∵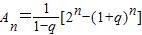 ,∴
,∴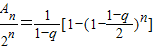 ,
,
当q充分接近于1时,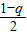 接近于0,由二项式定理知
接近于0,由二项式定理知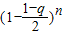 充分接近于
充分接近于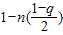 ,
,
所以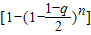 充分接近
充分接近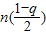 ,故
,故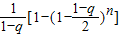 充分接近
充分接近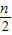 ,命题得证.
,命题得证.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.
(2)①先求得 an=1+q+q2+…+qn-1=
 ,可得An =
,可得An =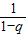 [(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)],再利用二项式系数的性质化简为
[(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)],再利用二项式系数的性质化简为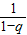 [2n-(1+q)n].
[2n-(1+q)n].②由①求得
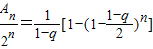 ,当q充分接近于1时,
,当q充分接近于1时,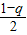 接近于0,由二项式定理知
接近于0,由二项式定理知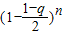 充分接近于
充分接近于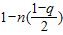 ,可得
,可得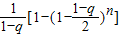 充分接近
充分接近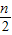 ,命题得证.
,命题得证.解答:解:(1)二项式
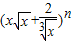 的展开式的通项公式为 Tr+1=
的展开式的通项公式为 Tr+1=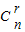 •
•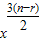 •2r•
•2r•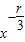 =
=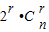 •
•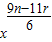 ,
,展开式中前3项系数的和为
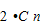 +
+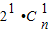 +
+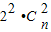 =129,解得n=8.
=129,解得n=8.故通项公式为 Tr+1=
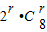 •
•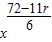 ,令
,令 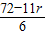 =0,自然数r无解,故展开式中没有常数项.
=0,自然数r无解,故展开式中没有常数项.令
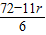 =1,解得自然数r=6,故有一次项,且一次项为1792x.
=1,解得自然数r=6,故有一次项,且一次项为1792x.(2)①因为q≠1,所以,an=1+q+q2+…+qn-1=
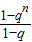 .
.于是,An=
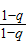
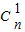 +
+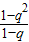
 +…+
+…+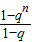 Cnn =
Cnn =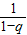 [(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]
[(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]=
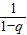 {(2n-1)-[(1+q)n-1]}=
{(2n-1)-[(1+q)n-1]}=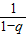 [2n-(1+q)n].
[2n-(1+q)n].②∵
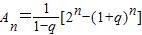 ,∴
,∴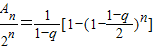 ,
,当q充分接近于1时,
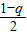 接近于0,由二项式定理知
接近于0,由二项式定理知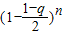 充分接近于
充分接近于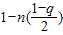 ,
,所以
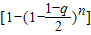 充分接近
充分接近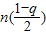 ,故
,故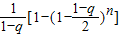 充分接近
充分接近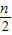 ,命题得证.
,命题得证.点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目