题目内容
已知动圆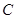 过点
过点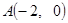 ,且与圆
,且与圆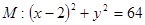 相内切,则动圆
相内切,则动圆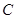 的圆心的轨迹方程_____________;
的圆心的轨迹方程_____________;
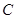 过点
过点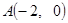 ,且与圆
,且与圆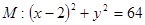 相内切,则动圆
相内切,则动圆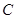 的圆心的轨迹方程_____________;
的圆心的轨迹方程_____________;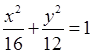
试题分析:因为动圆
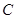 过点
过点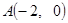 ,所以动圆的半径即为
,所以动圆的半径即为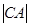 ,又因为动圆
,又因为动圆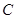 与圆
与圆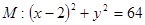 相内切,所以
相内切,所以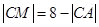 ,所以
,所以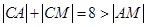 ,所以动圆
,所以动圆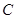 的圆心的轨迹为以
的圆心的轨迹为以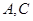 为焦点的椭圆,所以
为焦点的椭圆,所以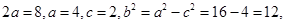 所以轨迹方程为
所以轨迹方程为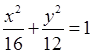 .
.点评:正确运用椭圆的定义是解决此题的关键,当然还要主要椭圆定义中的限制条件.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
题目内容
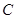 过点
过点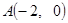 ,且与圆
,且与圆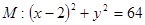 相内切,则动圆
相内切,则动圆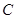 的圆心的轨迹方程_____________;
的圆心的轨迹方程_____________;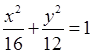
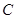 过点
过点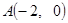 ,所以动圆的半径即为
,所以动圆的半径即为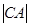 ,又因为动圆
,又因为动圆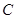 与圆
与圆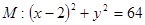 相内切,所以
相内切,所以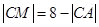 ,所以
,所以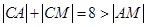 ,所以动圆
,所以动圆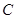 的圆心的轨迹为以
的圆心的轨迹为以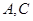 为焦点的椭圆,所以
为焦点的椭圆,所以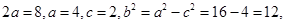 所以轨迹方程为
所以轨迹方程为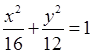 .
.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案