题目内容
已知圆 关于直线
关于直线 对称,圆心
对称,圆心 在第二象限,半径为
在第二象限,半径为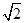 .
.
(1)求圆 的方程;
的方程;
(2)是否存在直线 与圆
与圆 相切,且在
相切,且在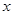 轴、
轴、 轴上的截距相等?若存在,求直线的方程;若不存在,说明理由。
轴上的截距相等?若存在,求直线的方程;若不存在,说明理由。
【答案】
(1)
(2) ,
, ,
, .
.
【解析】
试题分析:(1)由题意知:圆心(-1,2),半径 ,圆C:(x+1)2+(y-2)2=5.
,圆C:(x+1)2+(y-2)2=5.
(2)在 轴、
轴、 轴上的截距相等且不为0时,设存在直线
轴上的截距相等且不为0时,设存在直线 :
: 与圆
与圆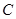 相切,则圆心到直线的距离为半径
相切,则圆心到直线的距离为半径 。所以,
。所以, ,
, 或3,直线方程为
或3,直线方程为 ,
, ;
;
在 轴、
轴、 轴上的截距相等且不为0时,设存在直线
轴上的截距相等且不为0时,设存在直线 :
: 与圆
与圆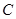 相切,则有
相切,则有 ,所以,
,所以,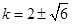 ,即
,即 ,综上知,存在直线
,综上知,存在直线 与圆
与圆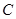 相切,且在
相切,且在 轴、
轴、 轴上的截距相等,直线方程为
轴上的截距相等,直线方程为 ,
, ,
, .
.
考点:圆的方程,直线与圆的位置关系。
点评:中档题,本题综合考查圆的方程,直线与圆的位置关系。在研究直线与圆的位置关系时,通常可选择“代数法”或“几何法”,圆的“特征直角三角形”更为常用。本题(2)易忽视截距为0的情况。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 .
. ~
~ ,那么
,那么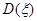 为5.
为5. ”为假命题,则p,q均为真命题.
”为假命题,则p,q均为真命题. 关于直线
关于直线  对称,则
对称,则
 .
. 关于直线
关于直线 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为 。
。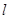 与圆C相切,且
与圆C相切,且 轴、
轴、 轴上的截距相等,求直线
轴上的截距相等,求直线 关于直线
关于直线 :
: 对称的圆为
对称的圆为 .
. 和圆
和圆  求线段
求线段 长的最小值.(12分)
长的最小值.(12分)