Question

如图，在自空间一点O出发引三条射线OA，OB，OC中，平面OAB垂直于平面OBC，设直线OA和平面OBC所成的角为θ；∠AOC=β；∠BOC=γ；二面角A-OC-B的平面角为φ则有下面四个命题，
①cosβ=cosθcosγ；
②cosθ=cosβcosγ；
③sinφ=sinθsinβ；
④sinθ=sinβsinφ其中正确命题的序号是

①，④

：（写出所有正确答案的序号）

Answer 1

分析：过A作AE⊥OB于E，过E作EF⊥OC于F，连接AF．则三棱锥A-OEF的四个面均为直角三角形．分别表示出各角的正弦，余弦，寻找验证个选项即可．

解答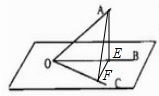：解：过A在面AOB内作AE⊥OB于E，∵平面OAB⊥平面OBC，平面OAB∩平面OBC=OB，根据平面和平面垂直的性质定理得知AE⊥平面OBC，∴∠AOE为直线OA和平面OBC所成的角．∴∠AOE=θ．
再过E作EF⊥OC于F，连接AF．由AE⊥平面OBC，OC?面OBC，∴AE⊥OC．
∵EF∩AE=F，∴OC⊥面AEF，
∵AF?面AEF，∴OC⊥AF．
所以cosβ=

OF

OA

，cosθ=

OE

OA

，cosγ=

OF

OE

，得出cosβ=cosθcosγ，①正确，②错误．
sinθ=

AE

OA

，sinβ=

AF

OA

，sinφ=

AE

AF

，得出sinθ=sinβsinφ，④正确，③错误．
综上所述，①④．
故答案为：①④．

点评：本题考查了空间角的度量与表示，考查空间想象能力．推理论证、运算求解能力．