题目内容
(川中班)(理)在极坐标系中,A(1,
),点B在直线ρcosθ+ρsinθ=0上运动,当线段AB长最短时,点B的极坐标为
(川中班)(文)实数x、y满足
,则k=
的取值范围为
(川中南校班)
(
)n=<u>
| π |
| 2 |
(
,
)
| ||
| 2 |
| 3π |
| 4 |
(
,
)
.
| ||
| 2 |
| 3π |
| 4 |
(川中班)(文)实数x、y满足
|
| y-1 |
| x+1 |
[-
,1)
| 1 |
| 2 |
[-
,1)
.| 1 |
| 2 |
(川中南校班)
| lim |
| n→∞ |
| n |
| n+2 |
e-2
e-2
.分析:(川中班)(理)将直线ρcosθ+ρsinθ=0化为一般方程,再利用线段AB最短可知直线AB与已知直线垂直,设出直线AB的方程,联立方程求出B的坐标,从而求解.
(川中班)(文)先作出实数x、y所表示的可行域然后将目标函数变为k=
则问题就转化为可行域内的动点(xy)与定点(-1,1)连线的斜率则根据图形即可求解.
(川中南校班)利用重要极限
(1+
)n=e进行求解.
(川中班)(文)先作出实数x、y所表示的可行域然后将目标函数变为k=
| y-1 |
| x-(-1) |
(川中南校班)利用重要极限
| lim |
| n→∞ |
| 1 |
| n |
解答:解::(川中班)(理)∵x=ρcosθ,y=ρsinθ,代入直线ρcosθ+ρsinθ=0,可得x+y=0…①
∵定点A(1,
)与动点B在直线ρcosθ+ρsinθ=0上运动
∴当线段AB最短时,此时直线AB垂直于直线x+y=0
设直线AB为:y-
=1×(x-1),即y=x-1+
…②
联立方程①②求得交点B(
-
,-
+
)
∴B极坐标为ρ=
=
,tanθ=
=-1
∴θ=-
∴B(
,
)
(川中班)(文)实数x、y满足
所表示的可行域如下图:
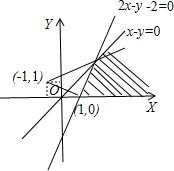
∵k=
=
表示可行域内的动点(x,y)与定点(-1,1)连线的斜率
∴
≤k<1即k∈[-
,1)
(川中南校班)
(
)n=
=
=
=e-2
∵定点A(1,
| π |
| 2 |
∴当线段AB最短时,此时直线AB垂直于直线x+y=0
设直线AB为:y-
| π |
| 2 |
| π |
| 2 |
联立方程①②求得交点B(
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
∴B极坐标为ρ=
| x2+y2 |
| ||
| 2 |
| y |
| x |
∴θ=-
| 3π |
| 4 |
∴B(
| ||
| 2 |
| 3π |
| 4 |
(川中班)(文)实数x、y满足
|

∵k=
| y-1 |
| x+1 |
| y-1 |
| x-(-1) |
∴
| 1-0 |
| -1-1 |
| 1 |
| 2 |
(川中南校班)
| lim |
| n→∞ |
| n |
| n+2 |
| lim |
| n→∞ |
| 1 | ||
(1+
|
| lim |
| n→∞ |
| 1 | ||||
[ (1+
|
| 1 | ||||||
(
|
点评:(川中班)(理)主要考查极坐标与一般方程之间的转化,是一道基础题,注意极坐标与一般方程的关系:ρ═
tanθ=
,x=ρcosθ,y=ρsinθ.
(川中班)(文)主要考察了线性规划.解题的关键是先做出可行域然后根据目标函数的几何意义进行求解.
(川中南校班)主要考察了重要极限
(1+
)n=e的应用.解题的关键是要将所求的极限等价变形成此重要极限的形式.
| x2+y2 |
| y |
| x |
(川中班)(文)主要考察了线性规划.解题的关键是先做出可行域然后根据目标函数的几何意义进行求解.
(川中南校班)主要考察了重要极限
| lim |
| n→∞ |
| 1 |
| n |

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目