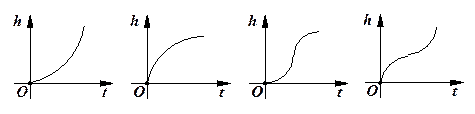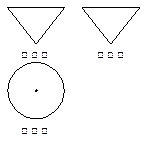题目内容
定义在R上的函数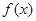 为奇函数,且
为奇函数,且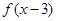 为偶函数.记
为偶函数.记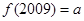 ,若
,若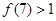 ,则一定有( )
,则一定有( )
A.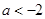 | B.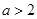 | C.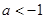 | D.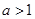 |
C
解析考点:函数奇偶性的性质.
专题:转化思想.
分析:由题设条件f(x-3)为偶函数可得函数f(x)关于x=-3对称,此条件与函数f(x)为奇函数相结合,可以求出函数的周期,利用周期性化简即可
解答:解:由题意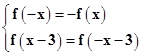
∴f(x-3)=f(-x-3)=-f(x+3)=f(x+9),∴T=12
故a=f(2009)=f(5)=f(-7)=-f(7),
∵f(7)>1,
∴a<-1
故选C
点评:本题考查函数奇偶性的性质,求解本题的关键是根据题设中的条件推证出函数的周期是12,把条件正确转化是能不能解决这个问题的关键,题后要总结条件转化的规律,近几年的高考中这一推理多次出现.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x,y满足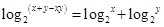 则x+y的取值范围为( )
则x+y的取值范围为( )
A.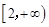 | B.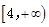 | C.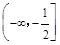 | D. |
函数y=3x+1(-1≤x<0)的反函数是( )
| A.y=1+log3x(x>0) | B.y=-1+log3x(x>0) |
| C.y=-1+log3x(1≤x<3) | D.y=-1+log3x(-1≤x<3) |
已知函数 的图像如图所示,则
的图像如图所示,则 的解析式可能是
的解析式可能是
A. | B. |
C. | D. |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.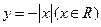 | B.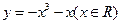 | C.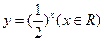 | D.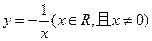 |
奇函数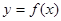 在区间[3,7]上是增函数,且最小值为-5,那么
在区间[3,7]上是增函数,且最小值为-5,那么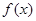 在区间[-7,-3]
在区间[-7,-3]
| A.是增函数且最小值为5 | B.是增函数且最大值为5 |
| C.是减函数且最小值为5 | D.是减函数且最大值为5 |
如果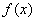 是定义在
是定义在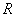 的增函数,且
的增函数,且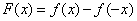 ,那么
,那么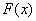 一定是
一定是
A.奇函数,且在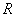 上是增函数 上是增函数 | B.奇函数,且在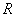 上是减函数 上是减函数 |
C.偶函数,且在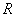 上是增函数 上是增函数 | D.偶函数,且在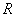 上是减函数 上是减函数 |
 为正三角形,四边形ABCD为正方形,平面
为正三角形,四边形ABCD为正方形,平面 .点M为平面ABCD内的一个动点,且满足
.点M为平面ABCD内的一个动点,且满足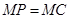 .则点M在正方形ABCD内的轨迹为
.则点M在正方形ABCD内的轨迹为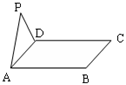
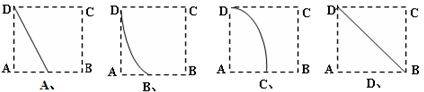
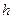 随时间
随时间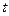 变化的可能图象是( )
变化的可能图象是( )