题目内容
设随机变量服从正态分布N(0,1),记φ(x)=P(ξ<x),则下列结论正确的是( )A.φ(0)=0
B.φ(0)=

C.φ(-x)=φ(x)
D.φ(-x)=-φ(x)
【答案】分析:根据随机变量ξ服从正态分布N(0,1),曲线关于ξ=0对称,根据φ(x)=p(ξ<x),把所给的四个结论变化整理,根据概率和正态曲线的性质,得到结果.
解答:解:随机变量ξ服从正态分布N(0,1),曲线关于ξ=0对称,
记φ(x)=p(ξ<x),给出下列结论:
A:φ(0)=P(ξ<0)=0.5;故A不正确,B正确.
C:φ(-x)=1-φ(x);故C、D不正确,
故选B
点评:本题考查正态分布的性质和简单的运算,是一个基础题,解题的关键是抓住正态分布的特点,内容比较简单,是一个送分题目.
解答:解:随机变量ξ服从正态分布N(0,1),曲线关于ξ=0对称,
记φ(x)=p(ξ<x),给出下列结论:
A:φ(0)=P(ξ<0)=0.5;故A不正确,B正确.
C:φ(-x)=1-φ(x);故C、D不正确,
故选B
点评:本题考查正态分布的性质和简单的运算,是一个基础题,解题的关键是抓住正态分布的特点,内容比较简单,是一个送分题目.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 服从正态分 布
服从正态分 布 ,若
,若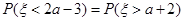 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.