题目内容
设集合Pn={1,2,…,n},n∈N*,记f(n)为同时满足下列条件的集合A的个数:
①A⊆Pn;
②若x∈A,则2x∉A;
③若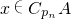 ,则
,则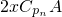 .
.
则f(4)=
- A.2
- B.3
- C.4
- D.5
C
分析:由已知中关于f(n)的定义,我们分1∈A和1∉A两种情况进行讨论,分别确定满足条件的A的个数,最后综合讨论结果,可得结论.
解答:但n=4时,P4={1,2,3,4},
若1∈A,则2∉A,则2∈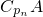 ,则4∉
,则4∉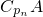 ,即4∈A,
,即4∈A,
此时A={1,4}或A={1,3,4}
若1∉A,1∈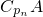 ,2∉
,2∉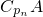 ,则2∈A,则4∉A,
,则2∈A,则4∉A,
此时A={2}或A={2,3}
故满足条件的集合A有4个
故选C
点评:本题考查的知识点是集合元素的确定,其中分类讨论,确定能确定的元素,然后列举满足条件的集合A的个数是解答的关键.
分析:由已知中关于f(n)的定义,我们分1∈A和1∉A两种情况进行讨论,分别确定满足条件的A的个数,最后综合讨论结果,可得结论.
解答:但n=4时,P4={1,2,3,4},
若1∈A,则2∉A,则2∈
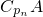 ,则4∉
,则4∉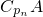 ,即4∈A,
,即4∈A,此时A={1,4}或A={1,3,4}
若1∉A,1∈
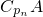 ,2∉
,2∉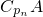 ,则2∈A,则4∉A,
,则2∈A,则4∉A,此时A={2}或A={2,3}
故满足条件的集合A有4个
故选C
点评:本题考查的知识点是集合元素的确定,其中分类讨论,确定能确定的元素,然后列举满足条件的集合A的个数是解答的关键.

练习册系列答案
相关题目
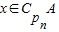 ,则
,则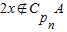 .
.