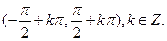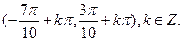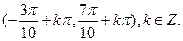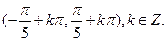题目内容
设函数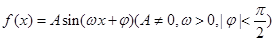 的图像关于直线
的图像关于直线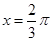 对称,且它的最小正周期为
对称,且它的最小正周期为 ,则 ( )
,则 ( )
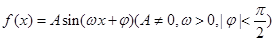 的图像关于直线
的图像关于直线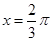 对称,且它的最小正周期为
对称,且它的最小正周期为 ,则 ( )
,则 ( )A.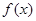 的图像经过点 的图像经过点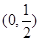 | B.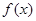 在区间 在区间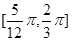 上是减函数 上是减函数 |
C.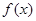 的图像的一个对称中心是 的图像的一个对称中心是 | D.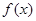 的最大值为A 的最大值为A |
C
专题:三角函数的图像与性质.
分析:根据周期求出ω,根据函数图象关于直线x=
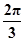 对称求出φ,可得函数的解析式,根据函数的解析式判断各个选项是否正确
对称求出φ,可得函数的解析式,根据函数的解析式判断各个选项是否正确解答:解:由题意可得
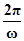 =π,∴ω=2,可得f(x)=Asin(2x+φ).
=π,∴ω=2,可得f(x)=Asin(2x+φ).再由函数图象关于直线x=
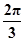 对称,故f(
对称,故f(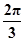 )=Asin(
)=Asin(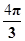 +φ)=±A,故可取φ=
+φ)=±A,故可取φ=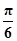 .
.故函数f(x)=Asin(2x+
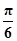 ).令2kπ+
).令2kπ+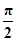 ≤2x+
≤2x+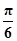 ≤2kπ+
≤2kπ+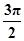 ,k∈z,求得kπ+
,k∈z,求得kπ+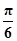 ≤x≤kπ+
≤x≤kπ+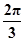 ,k∈z,故函数的减区间为[kπ+
,k∈z,故函数的减区间为[kπ+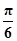 ,kπ+
,kπ+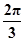 ],k∈z,故选项B不正确.
],k∈z,故选项B不正确.由于A不确定,故选项A不正确. 令2x+
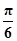 =kπ,k∈z,可得 x=
=kπ,k∈z,可得 x=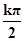 -
-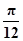 ,k∈z,
,k∈z,故函数的对称中心为 (
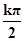 -
-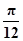 ,0),k∈z,故选项C正确.
,0),k∈z,故选项C正确.由于A的值的符号不确定,故选项D不正确.
故选C
点评:本题主要考查由函数y=Asin(ωx+φ )的部分图象求函数的解析式,正弦函数的对称性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
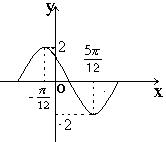
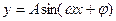 (
(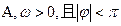 )在一个周期内的图象如右图,
)在一个周期内的图象如右图,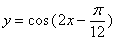 最小正周期是
最小正周期是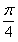
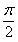
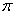
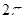
 是
是  且在[
且在[ ]内有且只有三个零点的函数;
]内有且只有三个零点的函数; 且在[
且在[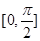 上的最大点是( )
上的最大点是( )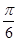
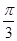
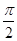
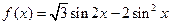 .
.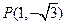 在角
在角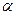 的终边上,求
的终边上,求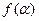 的值;
的值; 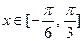 ,求
,求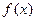 的值域.
的值域.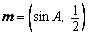 与
与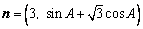 共线,其中A是△ABC的内角。
共线,其中A是△ABC的内角。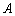 的大小;
的大小; 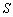 的最大值,并判断S取得最大值时△ABC的形状。
的最大值,并判断S取得最大值时△ABC的形状。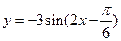 的单调递减区间为 ▲ .
的单调递减区间为 ▲ .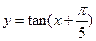 的单调区间是
的单调区间是