Question

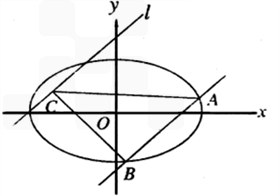
已知△ABC的顶点A、B在椭圆x²+3y²=4上,点C在直线l:y=x+2上,且AB∥l
（1）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（2）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程.

Answer 1

解：（1）因为AB∥l且AB通过原点（0，0），所以AB所在直线的方程为y=x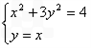
得A、B两点坐标分别是A（1，1），B（-1，-1）。
 ∴|AB|=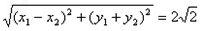 
∵AB边上的高h等于原点到直线的距离。
∴h=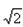,S_△ABC=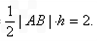      
（2）设AB所在直线的方程为y=x+m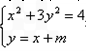
得4x²+6mx+3m²-4=0，
B两点在椭圆上，所以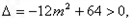 即，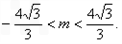
B两点坐标分别为（x₁，y₁），（x₂，y₂），
则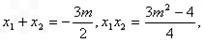
且y₁=x₁+m，y₂=x₂+m
∴|AB|=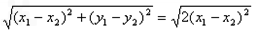
  
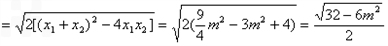
∵BC的长等于点（0，m）到直线l的距离，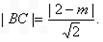
 
∴|AC|²=|AB|²+|BC|²=-m²-2m+10=11-（m+1）²
∴当m=-1时，AC边最长。（显然）        ，
AB所在直线的方程为y=x-1