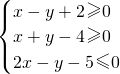题目内容
已知两实数x,y满足0≤x≤2,1≤y≤3.
(1)若x,y∈N,求使不等式2x-y+2>0成立的概率;
(2)若x,y∈R,求使不等式2x-y+2>0不成立的概率.
(1)若x,y∈N,求使不等式2x-y+2>0成立的概率;
(2)若x,y∈R,求使不等式2x-y+2>0不成立的概率.
分析:(1)本题是一个等可能事件的概率,利用列举法列出试验发生包含的事件数,列举出不等式2x-y+2>0要满足的事件数的结果,再利用概率公式计算即得.
(2)利用几何概型的计算概率的方法解决本题,关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积,通过相除的方法完成本题的解答.
(2)利用几何概型的计算概率的方法解决本题,关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积,通过相除的方法完成本题的解答.
解答: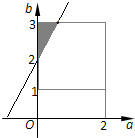 解:(Ⅰ)设“使不等式2x-y+2>0成立”为事件A (1分)
解:(Ⅰ)设“使不等式2x-y+2>0成立”为事件A (1分)
因为x,y∈N,(x,y)可有(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)共9种情况..(3分)
事件A有(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)7种可能. (4分)
∴P(A)=
(5分)
所以使不等式2x-y+2>0成立的概率为
; (6分)
(Ⅱ)设“使不等式2x-y+2>0不成立”也即“使不等式2x-y+2≤0成立”为事件B,
因为x∈[0,2],y∈[1,3],
所以(x,y)对应的区域边长为2的正方形(如图),面积为Ω=4 (8分)
2x-y+2≤0,对应的区域是如图阴影部分.
设面积为s=
×1×
=
(10分)P(B)=
=
=
. (11分)
故使不等式2x-y+2>0不成立的概率为
(12分)
 解:(Ⅰ)设“使不等式2x-y+2>0成立”为事件A (1分)
解:(Ⅰ)设“使不等式2x-y+2>0成立”为事件A (1分)因为x,y∈N,(x,y)可有(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)共9种情况..(3分)
事件A有(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)7种可能. (4分)
∴P(A)=
| 7 |
| 9 |
所以使不等式2x-y+2>0成立的概率为
| 7 |
| 9 |
(Ⅱ)设“使不等式2x-y+2>0不成立”也即“使不等式2x-y+2≤0成立”为事件B,
因为x∈[0,2],y∈[1,3],
所以(x,y)对应的区域边长为2的正方形(如图),面积为Ω=4 (8分)
2x-y+2≤0,对应的区域是如图阴影部分.
设面积为s=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| s |
| Ω |
| ||
| 4 |
| 1 |
| 16 |
故使不等式2x-y+2>0不成立的概率为
| 1 |
| 16 |
点评:本题主要考查几何概型中的面积类型和古典概型,两者最明显的区别是古典概型的基本事件是有限的,几何概型的基本事件是无限的.

练习册系列答案
相关题目