题目内容
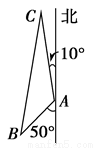
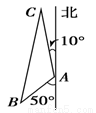
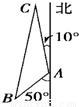
 我舰在敌岛A处南偏西50°的B处,发现敌舰正离开A岛沿北偏西10°的方向以每小时10海里的速度航行,我舰要用2小时的时间追赶敌舰,设图中的C处是我舰追上敌舰的地点,且已知AB距离为12海里.
我舰在敌岛A处南偏西50°的B处,发现敌舰正离开A岛沿北偏西10°的方向以每小时10海里的速度航行,我舰要用2小时的时间追赶敌舰,设图中的C处是我舰追上敌舰的地点,且已知AB距离为12海里.(1)求我舰追赶敌舰的速度;
(2)求∠ABC的正弦值.
分析:(1)在△ABC中,利用余弦定理求BC,即可求我舰追赶敌舰的速度;
(2)在△ABC中,利用正弦定理,即可求∠ABC的正弦值.
(2)在△ABC中,利用正弦定理,即可求∠ABC的正弦值.
解答:解:(1)在△ABC中,由已知,AC=10×2=20(海里),AB=12(海里),∠BAC=180°-50°-10°=120°.…(1分)
由余弦定理,得BC2=AB2+AC2-2AB•ACcos 120°=784,…(4分)
∴BC=28海里,…(5分)
∴v=14海里/小时. …(6分)
(2)在△ABC中,根据正弦定理,得
=
…(9分)
所以sin∠ABC=
=
=
.…(11分)
故∠ABC的正弦值是
.…(12分)
由余弦定理,得BC2=AB2+AC2-2AB•ACcos 120°=784,…(4分)
∴BC=28海里,…(5分)
∴v=14海里/小时. …(6分)
(2)在△ABC中,根据正弦定理,得
| AC |
| sin∠ABC |
| BC |
| sin∠BAC |
所以sin∠ABC=
| ACsin∠BAC |
| BC |
| 20sin120° |
| 28 |
5
| ||
| 14 |
故∠ABC的正弦值是
5
| ||
| 14 |
点评:本题考查余弦定理,考查正弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
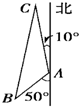 我舰在敌岛A处南偏西50°的B处,且AB距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求速度大小.
我舰在敌岛A处南偏西50°的B处,且AB距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求速度大小.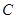 处是我舰追上敌舰的地点,且已知AB距离为12海里.
处是我舰追上敌舰的地点,且已知AB距离为12海里.