题目内容
已知平面α内有一个点A(2,-1,2),α的一个法向量为
=(3,1,2),则下列点P中,在平面α内的是( )
| n |
分析:由题意可知符合条件的点P应满足
•
=0,逐个选项验证即可.
| PA |
| n |
解答:解:由题意可知符合条件的点P应满足
•
=0,
选项A,
=(2,-1,2)-(1,-1,1)=(1,0,1),
•
=3×1+1×0+2×1=5≠0,故不在平面α内;
同理可得:选项B,
=(1,-4,
),
•
=0,故在平面α内;
选项C,
=(1,2,
),
•
=5≠0,故不在平面α内;
选项D,
=(3,-4,
),
•
=12≠0,故不在平面α内;
故选B
| PA |
| n |
选项A,
| PA |
| PA |
| n |
同理可得:选项B,
| PA |
| 1 |
| 2 |
| PA |
| n |
选项C,
| PA |
| 1 |
| 2 |
| PA |
| n |
选项D,
| PA |
| 7 |
| 2 |
| PA |
| n |
故选B
点评:本题考查平面法向量的定义,属基础题.

练习册系列答案
相关题目
已知平面α内有一个点M(1,-1,2),平面α的一个法向量是
=(6,-3,6),则下列点P中在平面α内的是( )
| n |
| A、P(2,3,3) |
| B、P(-2,0,1) |
| C、P(-4,4,0) |
| D、P(3,-3,4) |
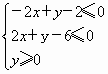 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M,此时的概率P为________.
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M,此时的概率P为________. 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M,此时的概率P为 .
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M,此时的概率P为 . =(6,-3,6),则下列点P中在平面α内的是( )
=(6,-3,6),则下列点P中在平面α内的是( )