题目内容
已知直线l过两直线3x-y-10=0和x+y-2=0的交点,且直线l与点A(1,3)和点B(5,2)的距离相等,求直线l的方程.
解:由 解得
解得 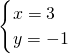 ,故两直线3x-y-10=0和x+y-2=0的交点M(3,-1).
,故两直线3x-y-10=0和x+y-2=0的交点M(3,-1).
当直线l平行于AB时,斜率等于KAB=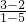 =-
=- ,
,
故直线l的方程为 y+1=- (x-3),即 x+4y+1=0.
(x-3),即 x+4y+1=0.
当直线l经过AB的中点N(3, )时,由于此时直线l经过M、N两点,且MN垂直于x轴,
)时,由于此时直线l经过M、N两点,且MN垂直于x轴,
故直线l的方程为 x=3.
综上,直线l的方程为 x+4y+1=0或x=3.
分析:解方程组求得两直线3x-y-10=0和x+y-2=0的交点M的坐标,直线l平行于AB时,用点斜式求直线方程.当直线l经过AB的中点N(3, )时,由MN垂直于x轴,求得直线l的方程.
)时,由MN垂直于x轴,求得直线l的方程.
点评:本题主要考查用点斜式求直线方程的方法,体现了分类讨论的数学思想,注意考虑直线过AB的中点N的情况,属于基础题.
 解得
解得 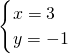 ,故两直线3x-y-10=0和x+y-2=0的交点M(3,-1).
,故两直线3x-y-10=0和x+y-2=0的交点M(3,-1).当直线l平行于AB时,斜率等于KAB=
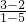 =-
=- ,
,故直线l的方程为 y+1=-
 (x-3),即 x+4y+1=0.
(x-3),即 x+4y+1=0.当直线l经过AB的中点N(3,
 )时,由于此时直线l经过M、N两点,且MN垂直于x轴,
)时,由于此时直线l经过M、N两点,且MN垂直于x轴,故直线l的方程为 x=3.
综上,直线l的方程为 x+4y+1=0或x=3.
分析:解方程组求得两直线3x-y-10=0和x+y-2=0的交点M的坐标,直线l平行于AB时,用点斜式求直线方程.当直线l经过AB的中点N(3,
 )时,由MN垂直于x轴,求得直线l的方程.
)时,由MN垂直于x轴,求得直线l的方程.点评:本题主要考查用点斜式求直线方程的方法,体现了分类讨论的数学思想,注意考虑直线过AB的中点N的情况,属于基础题.

练习册系列答案
相关题目
 已知直线l:y=2x与抛物线C:y=
已知直线l:y=2x与抛物线C:y=