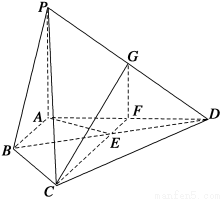
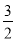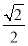题目内容
正项数列{an}的前n项和Sn满足：
－(n2＋n－1)Sn－(n2＋n)＝0.
(1)求数列{an}的通项公式an；
(2)令bn＝
，数列{bn}的前n项和为Tn，证明：对于任意的n∈N*，都有Tn<
.
（1）an＝2n（2）
【解析】(1)由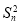
－(n2＋n－1)Sn－(n2＋n)＝0，得[Sn－(n2＋n)](Sn＋1)＝0，由于{an}是正项数列，所以Sn＋1>0.所以Sn＝n2＋n.n≥2时，an＝Sn－Sn－1＝2n，n＝1时，a1＝S1＝2适合上式．∴an＝2n.
(2)由an＝2n，得
bn＝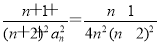
＝
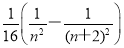
Tn＝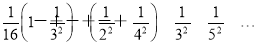
＝
<
＝
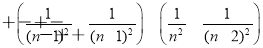
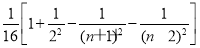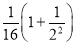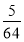
练习册系列答案
开心蛙口算题卡系列答案
相关题目
