题目内容
(12分)已知复数![]() 在复平面上对应的点为
在复平面上对应的点为![]() .
.
(Ⅰ)设集合![]() ,从集合
,从集合![]() 中随机取一个数作为
中随机取一个数作为![]() ,从集合
,从集合![]() 中随机取一个数作为
中随机取一个数作为![]() ,求复数
,求复数![]() 为纯虚数的概率;
为纯虚数的概率;
(Ⅱ)设![]() ,求点
,求点![]() 落在不等式组:
落在不等式组: 所表示的平面区域内的概率.
所表示的平面区域内的概率.
解析:(1)记 “复数![]() 为纯虚数”为事件
为纯虚数”为事件![]()
∵组成复数![]() 的所有情况共有12个:
的所有情况共有12个:![]() ,
,![]() ,
,
![]() ,
,![]() ,且每种情况出现的可能性相等,属于古典概型. ……2分
,且每种情况出现的可能性相等,属于古典概型. ……2分
其中事件![]() 包含的基本事件共2个:
包含的基本事件共2个: ![]() ………4分
………4分
∴所求事件的概率为![]() ………………6分
………………6分
(2)依条件可知,点![]() 均匀地分布在平面区域
均匀地分布在平面区域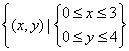 内,
内,
属于几何概型. 该平面区域的图形为右图中矩形![]() 围成的区域, 面积为
围成的区域, 面积为
![]() ……8分
……8分
所求事件构成的平面区域为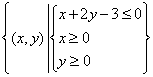 ,其图形如下图中的
,其图形如下图中的
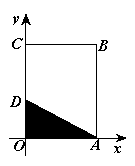
三角 第16题图
形![]() (阴影部分)
(阴影部分)
又直线![]() 与
与![]() 轴、
轴、![]() 轴的交点分别为
轴的交点分别为![]() ,
,
所以三角形![]() 的面积为
的面积为![]() ……10分
……10分
∴所求事件的概率为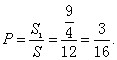 ………………12分
………………12分

练习册系列答案
相关题目
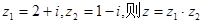 在复平面上对应的点位(
▲ )
在复平面上对应的点位(
▲ )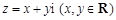 在复平面上对应的点为
在复平面上对应的点为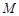 .
.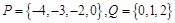 ,从集合
,从集合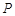 中随机取一个数作为
中随机取一个数作为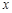 ,从集合
,从集合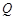 中随机取一个数作为
中随机取一个数作为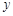 ,求复数
,求复数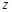 为纯虚数的概率;[来源:.COM][来源:.COM]
为纯虚数的概率;[来源:.COM][来源:.COM]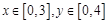 ,求点
,求点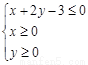 所表示的平面区域内的概率.
所表示的平面区域内的概率.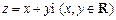 在复平面上对应的点为
在复平面上对应的点为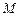 .
.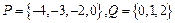 ,从集合
,从集合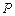 中随机取一个数作为
中随机取一个数作为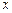 ,从集合
,从集合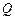 中随机取一个数作为
中随机取一个数作为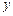 ,求复数
,求复数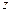 为纯虚数的概率;[来源:KS5U.COM][来源:KS5U.COM]
为纯虚数的概率;[来源:KS5U.COM][来源:KS5U.COM]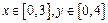 ,求点
,求点 所表示的平面区域内的概率.
所表示的平面区域内的概率.