题目内容
13．已知等腰△ABC的底边BC=2，腰AB=4，则腰上的中线长为$\sqrt{6}$．分析 根据三角形的性质，结合勾股定理求出B的余弦值，然后利用余弦定理即可得到结论．．
解答 解：∵等腰△ABC的底边BC=2，腰AB=4，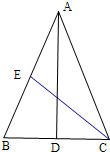
设D，E分别是BC，AB的中点，
∴AD⊥BC，BE=2，
即BD=1，则cosB=$\frac{BD}{AB}$=$\frac{1}{4}$，
则由余弦定理得CE2=BC2+BE2-2BC•BEcosB
=4+4-2×2×2×$\frac{1}{4}$=8-2=6，
即CE=$\sqrt{6}$，
故腰上的中线长为$\sqrt{6}$，
故答案为：$\sqrt{6}$
点评 本题主要考查解三角形的应用，根据条件求出cosB的值，利用余弦定理是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
3．若定义在R上的函数f（x）的导函数为f′（x），且满足f′（x）＞f（x），则f（2015）与f（2013）e2的大小关系为（ ）
| A． | f（2015）＜f（2013）e2 | B． | f（2015）=f（2013）e2 | C． | f（2015）＞f（2013）e2 | D． | 不能确定 |
4．设一个几何体的三视图如图所示，则这个几何体的体积为（ ）
| A． | 96 | B． | 48 | C． | 32 | D． | 24 |
1．最近高考改革方案已在上海和江苏开始实施，某教育机构为了了解我省广大师生对新高考改革的看法，对某市部分学校500名师生进行调查，统计结果如下：
在全体师生中随机抽取1名“赞成改革”的人是学生的概率为0.3，且z=2y．
（1）现从全部500名师生中用分层抽样的方法抽取50名进行问卷调查，则应抽取“不赞成改革”的教师和学生人数各是多少？
（2）在（1）中所抽取的“不赞成改革”的人中，随机选出三人进行座谈，求至少一名教师被选出的概率．
| 赞成改革 | 不赞成改革 | 无所谓 | |
| 教师 | 120 | y | 40 |
| 学生 | x | z | 130 |
（1）现从全部500名师生中用分层抽样的方法抽取50名进行问卷调查，则应抽取“不赞成改革”的教师和学生人数各是多少？
（2）在（1）中所抽取的“不赞成改革”的人中，随机选出三人进行座谈，求至少一名教师被选出的概率．
8．若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位后，得到的图象（ ）
| A． | 关于直线x=$\frac{π}{12}$对称 | B． | 关于直线x=$\frac{π}{6}$对称 | ||
| C． | 关于点（$\frac{π}{12}$，0）对称 | D． | 关于点（$\frac{π}{6}$，0）对称 |
5．复数z=$\frac{1-2i}{1+i}$（i为虚数单位）在复平面上对应的点的坐标为（ ）
| A． | （-$\frac{1}{2}$，-$\frac{3}{2}$i） | B． | （-$\frac{1}{2}$，-$\frac{3}{2}$） | C． | （-$\frac{3}{2}$，-$\frac{1}{2}$i） | D． | （$\frac{3}{2}$，-$\frac{1}{2}$） |
如图所示的四边形ABCD中，已知AB⊥AD，∠ABC=120°，∠ACD=60°，AD=27，设∠ACB=θ，C点到AD的距离为h．