题目内容
14.设点P(x,y)是曲线a|x|+b|y|=1(a≥0,b≥0)上任意一点,其坐标(x,y)均满足$\sqrt{{x^2}+{y^2}+4x+4}+\sqrt{{x^2}+{y^2}-4x+4}≤8$,则$2a+\sqrt{3}b$的取值范围为[1,+∞).分析 曲线a|x|+b|y|=1(a≥0,b≥0),对x,y分类讨论.画出图象:表示菱形ABCD.由$\sqrt{{x^2}+{y^2}+4x+4}+\sqrt{{x^2}+{y^2}-4x+4}≤8$,即$\sqrt{(x+2)^{2}+{y}^{2}}+\sqrt{(x-2)^{2}+{y}^{2}}≤8$.设M(-2,0),N(2,0),可得:2|PM|≤8,|BD|≤8,解出即可.
解答 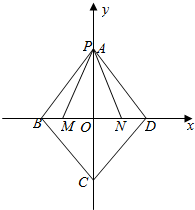 解:曲线a|x|+b|y|=1(a≥0,b≥0),
解:曲线a|x|+b|y|=1(a≥0,b≥0),
当x,y≥0时,化为ax+by=1;当x≥0,y≤0时,化为ax-by=1;
当x≤0,y≥0时,化为-ax+by=1;当x≤0,y≤0时,化为-ax-by=1.
画出图象:表示菱形ABCD.
由$\sqrt{{x^2}+{y^2}+4x+4}+\sqrt{{x^2}+{y^2}-4x+4}≤8$,即$\sqrt{(x+2)^{2}+{y}^{2}}+\sqrt{(x-2)^{2}+{y}^{2}}≤8$.
设M(-2,0),N(2,0),可得:2|PM|≤8,|BD|≤8,
∴$\sqrt{4+\frac{1}{{b}^{2}}}≤4$,$\frac{2}{a}≤8$,
解得b≥$\frac{\sqrt{3}}{6}$,a≥$\frac{1}{4}$,
∴$2a+\sqrt{3}b$$≥2×\frac{1}{4}+\sqrt{3}×\frac{\sqrt{3}}{6}=\frac{1}{2}+\frac{1}{2}=1$.
∴$2a+\sqrt{3}b$的取值范围为[1,+∞).
故答案为:[1,+∞).
点评 本题考查了直线方程、分类讨论思想方法、两点之间的距离公式,考查了数形结合思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知向量$\overrightarrow a$=(1,2),$\overrightarrow b$=(m,1),如果向量$\overrightarrow a$与$\overrightarrow b$平行,则m的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
9.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为:“x2=1,则x≠1” | |
| B. | 若命题p:?x∈R,x2-x+1<0,则命题¬p:?x∈R,x2-x+1>0 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “x2-5x-6=0”必要不充分条件是“x=-1” |
6.下列四个图象中,不能作为函数图象的是( )
| A. | 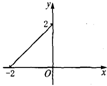 | B. | 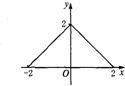 | C. |  | D. | 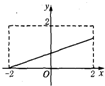 |
3.已知2x2+x-3=(x-1)(ax+b),则a,b的值分别为( )
| A. | 2,3 | B. | 2,-3 | C. | -2,3 | D. | -2,-3 |
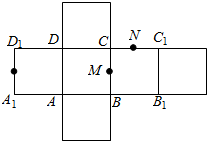 如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,
如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,