题目内容
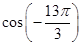 =(
)
=(
)
A.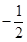 B.
B.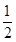 C.
C.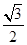 D.
D.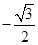
【答案】
B
【解析】
试题分析:
考点:三角函数诱导公式
点评:本题主要考查了三角函数诱导公式: ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
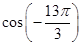 =(
)
=(
)
A.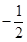 B.
B.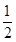 C.
C.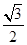 D.
D.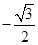
B
【解析】
试题分析:
考点:三角函数诱导公式
点评:本题主要考查了三角函数诱导公式: ,
,

 阅读快车系列答案
阅读快车系列答案