Question

设＝0是函数的一个极值点．

(1)求与的关系式(用表示)，并求f(x)的单 调区间；

(2)设，，问是否存在∈[－2，2]，使得成立？若存在，求的取值范围；若不存在，说明理由．

Answer 1

解：(1)

由得………………………2分

∴

令得

由于是极值点，故，即………………………4分

当时，，故的单调增区间是(－∞，0]和[，＋∞)，单调减区间是(0，)[

当时，，故的单调增区间是(－∞，]和[0，＋∞)，单调减区间是(,0)．………………………6分

(2)当时，<－2，在[－2,0]上单调递减，在[0,2]上单调递增，因此在[－2,2]上的值域为

[， ………………………7分

而在[－2,2]上单调递减，

所以值域是[，] ………………………8分

因为在[－2,2]上，

………………………9分

所以，只须满足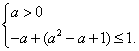………………………11分

解得

即当时，存在∈[－2，2]，使得成立．………………………12分