题目内容
已知函数 ,若有四个不同的正数
,若有四个不同的正数 满足
满足 (
( 为常数),且
为常数),且 ,
, ,则
,则 的值为( )
的值为( )
| A.10 | B.14 | C.12 | D.12或20 |
D
解析试题分析:函数 ,
, ,∵
,∵ ,故
,故 在两个周期之内竟然有四个解,∴
在两个周期之内竟然有四个解,∴ 在一个周期内有两个解,当
在一个周期内有两个解,当 时,四个根中其中两个关于
时,四个根中其中两个关于 对称,另两个关于
对称,另两个关于 对称,故其和为
对称,故其和为 , 当
, 当 时,四个根中其中两个关于
时,四个根中其中两个关于 对称,另两个关于
对称,另两个关于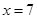 对称,故其和为
对称,故其和为 ,综上得:
,综上得: 12或20.
12或20.
考点:三角函数图像与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=2sin(ωx+φ)(ω>0,- <φ<
<φ< )的部分图象如图所示,则ω,φ的值分别是( )
)的部分图象如图所示,则ω,φ的值分别是( )
A.2,- | B.2,- |
C.4,- | D.4, |
为了得到函数 的图像,只需把函数
的图像,只需把函数 的图像上所有的点的( )
的图像上所有的点的( )
| A.横坐标伸长到原来的2倍,纵坐标不变 |
B.横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
| C.纵坐标伸长到原来的2倍,横坐标不变 |
D.纵坐标缩短到原来的 倍,横坐标不变 倍,横坐标不变 |
函数 的最小正周期是( )
的最小正周期是( )
A. | B. | C.2π | D.4π |
已知函数 的部分图象如右图所示,设
的部分图象如右图所示,设 是图象的最高点,
是图象的最高点, 是图象与
是图象与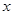 轴的交点,则
轴的交点,则 ( )
( )
A.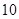 | B. | C. | D. |
 = ( )
= ( )
| A.4 | B.2 | C. | D. |
已知函数 ,在下列给出结论中:
,在下列给出结论中:
① 是
是 的一个周期;
的一个周期;
② 的图象关于直线
的图象关于直线
 对称;
对称;
③ 在
在 上单调递减.
上单调递减.
其中,正确结论的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
 满足
满足 ,则称
,则称 ; ②
; ② ;
;
 是三角形的内角).其中,为轮换对称式的个数是( )
是三角形的内角).其中,为轮换对称式的个数是( )



 的图象为( )
的图象为( )