题目内容
函数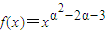 (常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .
(常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .
【答案】分析:根据幂函数的性质,要使得函数为偶函数,且在(0,+∞)上是单调递减函数,则α2-2α-3为偶数,且α2-2α-3<0,结合α∈Z 进行求解即可
解答:解:根据幂函数的性质,要使得函数为偶函数,且在(0,+∞)上是单调递减函数
则α2-2α-3为偶数,且α2-2α-3<0
解不等式可得,-1<α<3
∵α∈Z∴α=0,1,2
当α=0时,α2-2α-3=-3不满足条件
α=1时,α2-2α-3=-4满足条件
α=2时,α2-2α-3=-3不满足条件
故答案为:1
点评:本题主要考查了幂函数的性质:函数y=xα,为偶函数且在(0,+∞)单调递减的条件是α为偶数,且α<0,这是解决此题的关键.
解答:解:根据幂函数的性质,要使得函数为偶函数,且在(0,+∞)上是单调递减函数
则α2-2α-3为偶数,且α2-2α-3<0
解不等式可得,-1<α<3
∵α∈Z∴α=0,1,2
当α=0时,α2-2α-3=-3不满足条件
α=1时,α2-2α-3=-4满足条件
α=2时,α2-2α-3=-3不满足条件
故答案为:1
点评:本题主要考查了幂函数的性质:函数y=xα,为偶函数且在(0,+∞)单调递减的条件是α为偶数,且α<0,这是解决此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
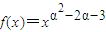 (常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .
(常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 . (常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .
(常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .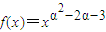 (常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .
(常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .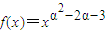 (常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .
(常数α∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则α的值为 .