题目内容
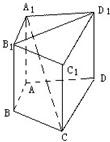 18、如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件
18、如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件
AC⊥BD
时,有A1C⊥B1D1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)分析:由四棱柱A1B1C1D1-ABCD是直棱柱?B1D1⊥A1A,若A1C⊥B1D1?B1D1⊥平面A1AC1C,下面结论就比较多了.
解答:解:∵四棱柱A1B1C1D1-ABCD是直棱柱,
∴B1D1⊥A1A,若A1C⊥B1D1
则B1D1⊥平面A1AC1C
∴BD⊥A1C
故答案为:BD⊥A1C.
∴B1D1⊥A1A,若A1C⊥B1D1
则B1D1⊥平面A1AC1C
∴BD⊥A1C
故答案为:BD⊥A1C.
点评:本题主要通过开放的形式来考查线线,线面,面面垂直关系的转化与应用.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2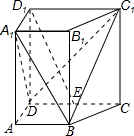 如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC. 如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC. 如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC. 如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.