题目内容
设抛物线![]() 的准线与
的准线与![]() 轴的交点为C,过点C作直线
轴的交点为C,过点C作直线![]() 交抛物线于A、B两点,求线段AB中点M的轨迹方程.
交抛物线于A、B两点,求线段AB中点M的轨迹方程.
解:∵抛物线准线与x轴交点C(0,1)
∴设直线![]() 的方程为y=kx+1 且A(x1,y1),B(x2,y2)
的方程为y=kx+1 且A(x1,y1),B(x2,y2)
由![]() ,得
,得![]()
∴x1+x2=-4k
∴y1+y2=k(x1+x2)+2=-4k2+2
![]() M(x,y)是AB的中点,
M(x,y)是AB的中点,
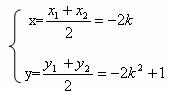
消去k得:![]()
∵![]() 交抛物线于两点,∴Δ=16k2-16>0 ∴k>1或k<-1 ∴x>2或x<-2
交抛物线于两点,∴Δ=16k2-16>0 ∴k>1或k<-1 ∴x>2或x<-2
故点M的轨迹方程为:![]() ( x>2或x<-2).
( x>2或x<-2).

练习册系列答案
相关题目
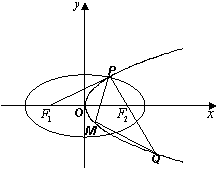 如图,设抛物线
如图,设抛物线