题目内容
用秦九韶方法求多项式f(x)= x7-2x6+3x3-4x2+1在x=2时的函数值.
解:f(x)= x7-2x6+3x3-4x2+1=((((((x-2)x+0)x+0)x+3)x-4)x+0)x+1.
由内向外逐次计算:
v0="1, " v1=v0x+a6="1×2-2=0, " v2=v1x+a5="0×2+0=0,"
v3=v2x+a4="0×2+0=0," v4=v3x+a3="0×2+3=3,"
v5=v4x+a2="3×2-4=2," v6=v5x+a1=2×2+0=4,
v7=v6x+a0=4×2+1=9.
故f(2)=9.
由内向外逐次计算:
v0="1, " v1=v0x+a6="1×2-2=0, " v2=v1x+a5="0×2+0=0,"
v3=v2x+a4="0×2+0=0," v4=v3x+a3="0×2+3=3,"
v5=v4x+a2="3×2-4=2," v6=v5x+a1=2×2+0=4,
v7=v6x+a0=4×2+1=9.
故f(2)=9.
根据秦九韶算法的操作方法,先将多项式f(x)进行改写,再逐步求值.
【题型解答题
【题型解答题

练习册系列答案
相关题目
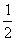 ,
, ,
, ,…,
,…, ,设计框图实现求该列数前20项的和.
,设计框图实现求该列数前20项的和.  按从大到小的顺序排序,
按从大到小的顺序排序, 时,实际是插入哪两个数之间( )
时,实际是插入哪两个数之间( ) 与
与

 与
与 =" " ▲
=" " ▲ 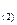 .
.