题目内容
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.(Ⅰ)写出抛物线C2的标准方程;
(Ⅱ)若
| AM |
| 1 |
| 2 |
| MB |
(Ⅲ)若坐标原点O关于直线l的对称点P在抛物线C2上,直线l与椭圆C1有公共点,求椭圆C1的长轴长的最小值.
分析:(Ⅰ)抛物线C2有公共焦点F(1,0),可知该抛物线的标准方程的形式和P的值,代入即可;
(Ⅱ)设出直线l的方程为y=k(x-4),联立方程,消去x,得到关于y的一元二次方程,设A(x1,y1),B(x2,y2),利用韦达定理和△>0及
=
,消去y1,y2,可求得斜率k的值;
(Ⅲ)设P(m,n),则OP中点为(
,
),因为O、P两点关于直线y=k(x-4)对称,利用对称的性质(垂直求平方),可求得斜率k的值,联立直线与椭圆方程,消去y,得到关于x的一元二次方程,△≥0,解不等式即可椭圆C1的长轴长的最小值.
(Ⅱ)设出直线l的方程为y=k(x-4),联立方程,消去x,得到关于y的一元二次方程,设A(x1,y1),B(x2,y2),利用韦达定理和△>0及
| AM |
| 1 |
| 2 |
| MB |
(Ⅲ)设P(m,n),则OP中点为(
| m |
| 2 |
| n |
| 2 |
解答: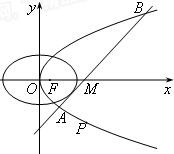 解:(Ⅰ)∵抛物线C2的焦点F(1,0),
解:(Ⅰ)∵抛物线C2的焦点F(1,0),
∴
=1,即p=2
∴抛物线C2的方程为:y2=4x,
(Ⅱ)设直线AB的方程为:y=k(x-4),(k存在且k≠0).
联立
,消去x,得ky2-4y-16k=0,
显然△=16+64k2>0,设A(x1,y1),B(x2,y2),
则y1+y2=
①y1•y2=-16 ②
又
=
,所以y1=-
y2 ③
由①②③消去y1,y2,得k2=2,
故直线l的方程为y=
x-4
,或y=-
x+4
.
(Ⅲ)设P(m,n),则OP中点为(
,
),因为O、P两点关于直线y=k(x-4)对称,
所以
,即
,解之得
,
将其代入抛物线方程,得:(-
)2=4•
,所以,k2=1.
联立
,消去y,得:(b2+a2k2)x2-8k2a2x+16a2k2-a2b2=0.
由△=(-8k2a2)2-4(b2+a2k2)(16a2k2-a2b2)≥0,
得16a2k4-(b2+a2k2)(16k2-b2)≥0,
即a2k2+b2≥16k2,
将k2=1,b2=a2-1代入上式并化简,得2a2≥17,所以a≥
,即2a≥
,
因此,椭圆C1长轴长的最小值为
.
 解:(Ⅰ)∵抛物线C2的焦点F(1,0),
解:(Ⅰ)∵抛物线C2的焦点F(1,0),∴
| p |
| 2 |
∴抛物线C2的方程为:y2=4x,
(Ⅱ)设直线AB的方程为:y=k(x-4),(k存在且k≠0).
联立
|
显然△=16+64k2>0,设A(x1,y1),B(x2,y2),
则y1+y2=
| 4 |
| k |
又
| AM |
| 1 |
| 2 |
| MB |
| 1 |
| 2 |
由①②③消去y1,y2,得k2=2,
故直线l的方程为y=
| 2 |
| 2 |
| 2 |
| 2 |
(Ⅲ)设P(m,n),则OP中点为(
| m |
| 2 |
| n |
| 2 |
所以
|
|
|
将其代入抛物线方程,得:(-
| 8k |
| 1+k2 |
| 8k2 |
| 1+k2 |
联立
|
由△=(-8k2a2)2-4(b2+a2k2)(16a2k2-a2b2)≥0,
得16a2k4-(b2+a2k2)(16k2-b2)≥0,
即a2k2+b2≥16k2,
将k2=1,b2=a2-1代入上式并化简,得2a2≥17,所以a≥
| ||
| 2 |
| 34 |
因此,椭圆C1长轴长的最小值为
| 34 |
点评:此题是个难题.本题考查了椭圆与抛物线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.其中问题(Ⅲ)考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(本小题满分12分)
已知椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从它们每条曲线上至少取两个点,将其坐标记录于下表中:
|
x |
5 |
- |
4 |
|
|
|
y |
2 |
0 |
-4 |
|
- |
(Ⅰ)求C1和C2的方程;
(Ⅱ)过点S(0,- )且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
)且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.






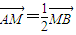 ,求直线l的方程;
,求直线l的方程;