题目内容
运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择.它们的速度分别为50千米/小时,100千米/小时,500千米/小时,每千米的运费分别为a元、b元、c元,且b<a<c.又这批海鲜在运输过程中的损耗为500元/小时,若使用三种运输工具分别运输时各自的总费用(运费与损耗之和)互不相等,试确定使用哪种运输工具总费用最省.(题中字母均为正的已知量)
解:设运输路程为S(千米),使用汽车、火车、飞机三种运输工具运输时,
各自的总费用分别为y1(元)、y2(元)、y3(元).则由题意,
 =
=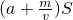 ,
,
y2=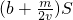 ,
,
y3=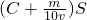
由a>b,各字母均为正值,
所以y1-y2>0,即y2<y1.
由y3-y2=[(c-b)-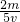 ]S.
]S.
令y3-y2>0,由c>b及每字母都是正值,
得c>b+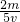 .
.
所以,当c>b+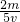 时y2<y3,由y2<y1,即y2最小,
时y2<y3,由y2<y1,即y2最小,
当b<a<c<b+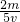 时,y3<y2<y1,y3最小.
时,y3<y2<y1,y3最小.
即当c>b+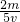 时,用火车运输总费用最省;当c<b+
时,用火车运输总费用最省;当c<b+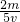 时,用飞机运输总费用最省;
时,用飞机运输总费用最省;
分析:要确定定使用哪种运输工具总费用最省,我们可以分别构造三个函数计算三种运输方式的费用,然后构造不等式,讨论三种运输方式下运输工具总费的大小关系,最小的即为最省的运输模式.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.
各自的总费用分别为y1(元)、y2(元)、y3(元).则由题意,
 =
=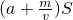 ,
,y2=
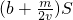 ,
,y3=
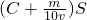
由a>b,各字母均为正值,
所以y1-y2>0,即y2<y1.
由y3-y2=[(c-b)-
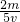 ]S.
]S.令y3-y2>0,由c>b及每字母都是正值,
得c>b+
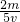 .
.所以,当c>b+
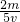 时y2<y3,由y2<y1,即y2最小,
时y2<y3,由y2<y1,即y2最小,当b<a<c<b+
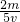 时,y3<y2<y1,y3最小.
时,y3<y2<y1,y3最小.即当c>b+
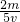 时,用火车运输总费用最省;当c<b+
时,用火车运输总费用最省;当c<b+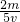 时,用飞机运输总费用最省;
时,用飞机运输总费用最省;分析:要确定定使用哪种运输工具总费用最省,我们可以分别构造三个函数计算三种运输方式的费用,然后构造不等式,讨论三种运输方式下运输工具总费的大小关系,最小的即为最省的运输模式.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目