题目内容
(1)观察下列各式:
>
;
>
;
>
;
>
…请你根据上述特点,提炼出一个一般性命题(写出已知,求证),并用分析法加以证明.
(2)命题p:已知a>0且a≠1,函数y=log2x单调递减,命题q:f(x)=x2-2ax+1(
,+∞)上为增函数,若“p∧q”为假,“p∨q”为真,求实数a的取值范围.
| 1+0.1 |
| 2+0.1 |
| 1 |
| 2 |
0.2+
| ||
0.5+
|
| 0.2 |
| 0.5 |
| ||
|
| ||
|
| 72+π |
| 101+π |
| 72 |
| 101 |
(2)命题p:已知a>0且a≠1,函数y=log2x单调递减,命题q:f(x)=x2-2ax+1(
| 1 |
| 2 |
分析:(1)分析已知条件中:
>
;
>
;…我们可以发现对于一个分式,分子和分母都加上同一个数后,其值变大,由此不难得到结论.
(2)依题意可分别求得命题p为真命题与命题q为真命题时a的取值范围,再结合题意,利用真值表通过解不等式组即可求得实数a的取值范围.
| 1+0.1 |
| 2+0.1 |
| 1 |
| 2 |
0.2+
| ||
0.5+
|
| 0.2 |
| 0.5 |
(2)依题意可分别求得命题p为真命题与命题q为真命题时a的取值范围,再结合题意,利用真值表通过解不等式组即可求得实数a的取值范围.
解答:解:(1)已知a>b>0,m>0,求证
>
…(3分)
证明:分析法a>b>0,m>0,
欲证:
>
只需证:a(b+m)>b(a+m)
只需证:ab+am>ab+bm
只需证:am>bm
只需证:a>b
由已知a>b成立
所以
>
成立…(6分)
(2)由命题P可知0<a<1…(7分)
由命题q:f(x)=(x-a)2+1-a2在(
,+∞)上为增函数,∴a≤
…(8分)
由命题p或q为真命题,命题p且q为假命题,可知命题p、q为真命题恰好一真一假,
(i)p真,q假时,
,∴
<a<1;
(ii)p假,q真时,
∴a∈∅…(11分)
综上:a的范围(
,1)…(12分)
| b+m |
| a+m |
| b |
| a |
证明:分析法a>b>0,m>0,
欲证:
| b+m |
| a+m |
| b |
| a |
只需证:a(b+m)>b(a+m)
只需证:ab+am>ab+bm
只需证:am>bm
只需证:a>b
由已知a>b成立
所以
| b+m |
| a+m |
| b |
| a |
(2)由命题P可知0<a<1…(7分)
由命题q:f(x)=(x-a)2+1-a2在(
| 1 |
| 2 |
| 1 |
| 2 |
由命题p或q为真命题,命题p且q为假命题,可知命题p、q为真命题恰好一真一假,
(i)p真,q假时,
|
| 1 |
| 2 |
(ii)p假,q真时,
|
综上:a的范围(
| 1 |
| 2 |
点评:本题主要考查了复合命题的真假、归纳推理.归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),(3)论证.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
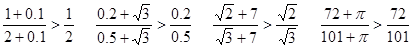
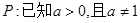 ,函数
,函数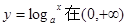 单调递减,
单调递减, 上为增函数,若“
上为增函数,若“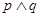 ”为假,“
”为假,“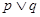 ”为真,求实数
”为真,求实数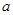 的取值范围。
的取值范围。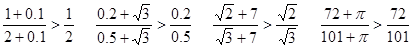
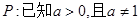 ,函数
,函数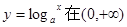 单调递减,
单调递减,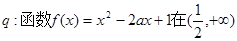 上为增函数,若“
上为增函数,若“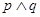 ”为假,“
”为假,“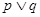 ”为真,求实数
”为真,求实数 的取值范围。
的取值范围。