题目内容
若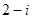 是关于
是关于 的实系数方程
的实系数方程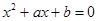 的一根,则该方程两根的模的和为( )
的一根,则该方程两根的模的和为( )
A.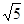 | B.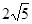 | C.5 | D.10 |
B
解析试题分析:因为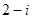 是关于
是关于 的实系数方程
的实系数方程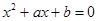 的一根,所以
的一根,所以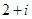 是该方程的另一个根,所以该方程两根的模的和为
是该方程的另一个根,所以该方程两根的模的和为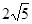 .
.
考点:本小题主要考查实系数方程的复数根的性质和复数的模的运算,考查学生分析问题解决问题的能力和运算求解能力.
点评:实系数方程的两个复数根互为共轭复数.

练习册系列答案
相关题目
i(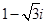 )=( )
)=( )
A.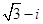 | B.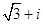 | C. | D. |
已知复数 ,则下列说法正确的是( )
,则下列说法正确的是( )
| A.复数z在复平面上对应的点在第二象限 |
B.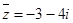 |
C. |
| D.复数z的实部与虚部之积为 —12 |
复数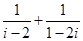 的虚部为 ( )
的虚部为 ( )
A.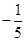 | B.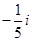 | C. | D.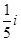 |
设复数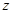 满足
满足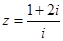 (
(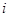 为虚数单位),则复数
为虚数单位),则复数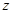 在复平面内对应的点位于
在复平面内对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
如果复数 的实部和虚部互为相反数,那么实数
的实部和虚部互为相反数,那么实数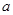 等于 ( )
等于 ( )
A.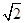 | B.2 | C.-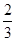 | D.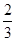 |
若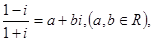 则
则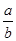 的值是 ( )
的值是 ( )
| A.1 | B.0 | C.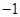 | D. |
已知集合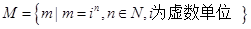 ,则下面属于
,则下面属于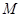 的元素是
的元素是
A. | B.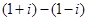 |
C.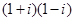 | D.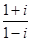 |
设 是实数,且
是实数,且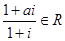 ,则实数
,则实数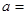 ( )
( )
A.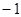 | B.1 | C.2 | D.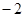 |