题目内容

过椭圆C：
x2
a2
+
y2
b2
=1的左焦点作直线l⊥x轴，交椭圆C于A，B两点，若△OAB（O为坐标原点）是直角三角形，则椭圆C的离心率e为（　　）
A、
3
-1
2
B、
3
+1
2
C、
5
-1
2
D、
5
+1
2
分析：首先求出A、B两点坐标，进而求出/AB/、/AO/、/BO/的长，再根据△OAB是直角三角形得出/AB/2=/AO/2+/BO/2即b2=ac，然后由b2=a2-c2，求出离心率．
解答：解：由题意知A（-c，
b2
a
） B（-c，-
b2
a
）
∴/AB/=2
b2
a
 AO=BO=
c2+(
b2
a
)2

∵△OAB是直角三角形
∴/AB/2=/AO/2+/BO/2
即
4b4
a2
=2c2+
2b4
a2

整理得b2=ac
∵b2=a2-c2
∴e2+e-1=0
又∵e＞0
∴e=
5
-1
2

故选C．
点评：本题考查了椭圆的性质，以及直角三角形的有关知识，解题过程注意e＞0，属于中档题．
练习册系列答案
相关题目
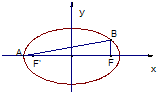过椭圆C：
x2
a
2
 
+
y2
b
2
 
=1(a＞b＞0)的一个顶点作圆x2+y2=b2的两条切线，切点分别为A，B，若∠AOB=90°（O是坐标原点），则椭圆C的离心率为
 
．
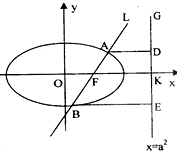精英家教网过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左顶点A的斜率为k的直线交椭圆C于另一个点B，且点B在x轴上的射影恰好为右焦点F，若
1
3
＜k＜
1
2
，则椭圆离心率的取值范围是
 
．
（2003•朝阳区一模）已知：如图，过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点F（-c，0）作垂直于长轴A1A2的直线与椭圆c交于P、Q两点，l为左准线．
（Ⅰ）求证：直线PA2、A1Q、l共点；
（Ⅱ）若过椭圆c左焦点F（-c，0）的直线斜率为k，与椭圆c交于P、Q两点，直线PA2、A1Q、l是否共点，若共点请证明，若不共点请说明理由．
（2010•龙岩二模）过椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点F且垂直于x轴的直线交椭圆于点(-1，
2
2
)．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在过点A（-2，0）的直线l与椭圆C交于两点M、N，使得|FP|=
1
2
|MN|（其中P为弦MN的中点）？若存在，求出直线l的方程；若不存在，请说明理由．
精英家教网如图，已知直线L：x=my+1过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点F，且交椭圆C于A、B两点，点A、B在直线G：x=a2上的射影依次为点D、E．
（1）若抛物线x2=4
3
y的焦点为椭圆C的上顶点，求椭圆C的方程；
（2）若N(
a2+1
2
，0)为x轴上一点，求证：
AN
=λ
NE
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网