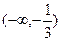题目内容
在平面直角坐标系中,若两个不同的点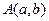 ,
,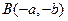 均在函数
均在函数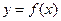 的图象上,则称
的图象上,则称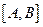 为函数
为函数 的一组关于原点的中心对称点(
的一组关于原点的中心对称点(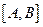 与
与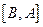 看作同一组),函数
看作同一组),函数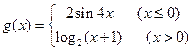 关于原点的中心对称点的组数为
关于原点的中心对称点的组数为
A.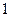 | B.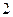 | C.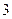 | D.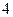 |
C
解析

练习册系列答案
相关题目
设偶函数f(x)满足f(x)="2x-4" (x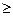 0),则
0),则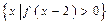 为( )
为( )
A.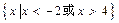 | B.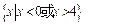 |
C.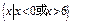 | D. |
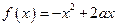 与
与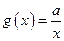 在
在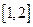 上都为减函数,则
上都为减函数,则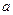 范围是( )
范围是( )
A. | B.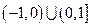  | C.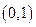 | D.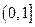 |
下列四个函数之中,在(0,+∞)上为增函数的是( )
A.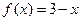 | B.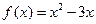 | C.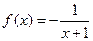 | D.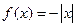 |
下列各组函数中,表示同一函数的是( )
⑴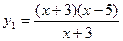 ,
,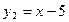 ;
;
⑵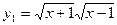 ,
,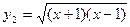 ;
;
⑶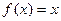 ,
,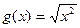 ;
;
⑷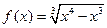 ,
,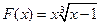 ;
;
⑸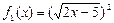 ,
,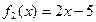 。
。
| A.⑴、⑵ | B.⑵、⑶ | C.⑷ | D.⑶、⑸ |
已知函数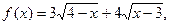 则函数
则函数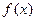 的最大值为 ( )
的最大值为 ( )
| A.3 | B.4 | C.5 | D.不存在 |
函数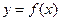 的图象与
的图象与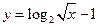 的图象关于直线
的图象关于直线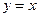 对称,则
对称,则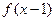 =( )
=( )
A.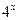 | B.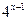 | C.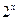 | D.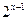 |
已 知
知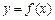 是偶函数,当
是偶函数,当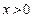 时,
时,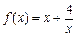 ,且当
,且当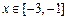 时,
时,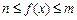 恒成立,则
恒成立,则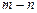 的最小值是( )
的最小值是( )
A.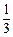 | B.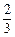 | C.1 | D.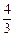 |
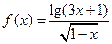 的定义域是 ( )
的定义域是 ( )
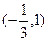
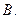
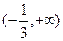 C.
C. D.
D.