题目内容
求和: = .(n∈N*)
= .(n∈N*)
【答案】分析:根据 (1+x)n= +
+ +
+ +…+
+…+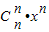 ,两边同时对x求导,再令 x=1,可得答案.
,两边同时对x求导,再令 x=1,可得答案.
解答:解:∵(1+x)n=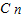 +
+ +
+ +…+
+…+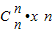 ,
,
两边同时对x求导可得 n(1+x)n-1=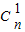 +2
+2 +3
+3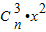 +…+n
+…+n .
.
令 x=1可得,n•2n-1= ,
,
故答案为 n•2n-1.
点评:本题主要考查二项式定理的应用,求函数的导数,属于中档题.
 +
+ +
+ +…+
+…+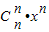 ,两边同时对x求导,再令 x=1,可得答案.
,两边同时对x求导,再令 x=1,可得答案.解答:解:∵(1+x)n=
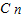 +
+ +
+ +…+
+…+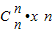 ,
,两边同时对x求导可得 n(1+x)n-1=
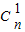 +2
+2 +3
+3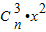 +…+n
+…+n .
.令 x=1可得,n•2n-1=
 ,
,故答案为 n•2n-1.
点评:本题主要考查二项式定理的应用,求函数的导数,属于中档题.

练习册系列答案
相关题目
已知等差数列{an}的首项为4,公差为4,其前n项和为Sn,则数列 {![]() }的前n项和为( )
}的前n项和为( )
|
| A. |
| B. |
| C. |
| D. |
|
| 考点: | 数列的求和;等差数列的性质. |
| 专题: | 等差数列与等比数列. |
| 分析: | 利用等差数列的前n项和即可得出Sn,再利用“裂项求和”即可得出数列 { |
| 解答: | 解:∵Sn=4n+ ∴ ∴数列 { 故选A. |
| 点评: | 熟练掌握等差数列的前n项和公式、“裂项求和”是解题的关键. |