题目内容
3.已知f(x)=$\frac{\sqrt{3}}{2}$cos2ωx-sinωxcosωx+$\frac{\sqrt{3}}{2}$(ω>0)的图象与直线y=m(m>0)相切,并且相邻两切点的横坐标相差2π.(Ⅰ)求ω和m的值;
(Ⅱ)△ABC中,角A,B,C的对边分别是a,b,c,若角A满足f(A)=-$\frac{\sqrt{3}}{2}$,且a=4,b+c=6,求△ABC的面积.
分析 (Ⅰ)由三角函数公式化简可得f(x)=cos(2ωx+$\frac{π}{6}$),由三角函数图象和周期性可得;
(Ⅱ)由(Ⅰ)结合三角形内角的范围可得A=$\frac{2π}{3}$,由余弦定理整体可得bc的值,代三角形的面积公式可得.
解答 解:(Ⅰ)由三角函数公式化简可得:
f(x)=$\frac{\sqrt{3}}{2}$cos2ωx-sinωxcosωx+$\frac{\sqrt{3}}{2}$
=$\frac{\sqrt{3}}{2}$cos2ωx-$\frac{1}{2}$sin2ωx+$\frac{\sqrt{3}}{2}$=cos(2ωx+$\frac{π}{6}$),
由题意可得m=1,$\frac{2π}{2ω}$=2π,解得ω=$\frac{1}{2}$;
(Ⅱ)由(Ⅰ)可得f(A)=cos(A+$\frac{π}{6}$)=-$\frac{\sqrt{3}}{2}$,
∴结合三角形内角的范围可得A+$\frac{π}{6}$=$\frac{5π}{6}$,A=$\frac{2π}{3}$,
由余弦定理可得a2=b2+c2-2bccosA=(b+c)2-2bc-2bccosA,
代入已知数据可得16=36-2bc-2bc(-$\frac{1}{2}$),解得bc=20,
∴△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}×20×\frac{\sqrt{3}}{2}$=5$\sqrt{3}$.
点评 本题考查三角函数恒等变换,涉及余弦定理和三角形的面积公式,属中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
12.下列各组函数f(x)与g(x)的图象相同的是( )
| A. | f(x)=x,g(x)=($\sqrt{x}$)2 | B. | $f(x)=\frac{{{x^2}-4}}{x-2}$与g(x)=x+2 | ||
| C. | f(x)=1,g(x)=x0 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,(x≥0)}\\{-x,(x<0)}\end{array}\right.$ |
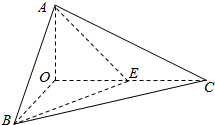 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.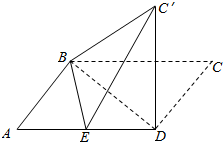 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.