题目内容
已知下列三组条件：（1）A：α=
，B：sinα=
；（2）A：x=1，B：x2+（a2-1）x-a2=0（a为实常数）；（3）A：定义域为R上的函数f（x）满足f（1）＞f（2），B：定义域为R的函数f（x）是单调减函数．其中A是B的充分不必要条件的是______．（填写所有满足要求的条件组的序号）
| π |
| 6 |
| 1 |
| 2 |
（1）∵sin
=
，即由A能推出B，反之不成立，比如sin
=
，但α≠
．A是B的充分不必要条件
（2）当x=1时，x2+（a2-1）x-a2=0，反之当a=0时，方程x2-x=0的根是1，0．由B推不出A．A是B的充分不必要条件
（3）函数f（x）=-x2满足A，但在定义域R上不是减函数，A不是B的充分条件
故答案为：（1）（2）
| π |
| 6 |
| 1 |
| 2 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
（2）当x=1时，x2+（a2-1）x-a2=0，反之当a=0时，方程x2-x=0的根是1，0．由B推不出A．A是B的充分不必要条件
（3）函数f（x）=-x2满足A，但在定义域R上不是减函数，A不是B的充分条件
故答案为：（1）（2）
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
，
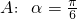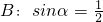；（2）A：x=1，B：x2+（a2-1）x-a2=0（a为实常数）；（3）A：定义域为R上的函数f（x）满足f（1）＞f（2），B：定义域为R的函数f（x）是单调减函数．其中A是B的充分不必要条件的是________．（填写所有满足要求的条件组的序号）
，
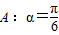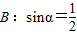；（2）A：x=1，B：x2+（a2-1）x-a2=0（a为实常数）；（3）A：定义域为R上的函数f（x）满足f（1）＞f（2），B：定义域为R的函数f（x）是单调减函数．其中A是B的充分不必要条件的是 ．（填写所有满足要求的条件组的序号）
，
；（2）
，
（
为实常数）；
定义域为
上的函数
满足
，
定义域为