题目内容
成都某中学2011年进行评定高级职称工作时,数学组、语文组各有2人够资格,能评上高级职称的可能性分别为| 2 |
| 3 |
| 1 |
| 2 |
(1)求这两个组各有1人评上的概率;
(2)求这两个组至少有1人评上的概率;
(3)求数学组评上的人数ξ的期望和方差.
分析:(1)由题意设Ak表示数学组评上k人(k=0,1,2),设Bi表示语文组评上i人(i=0,1,2),利用独立事件同时发生的定义及独立事件同时发生的概率公式即可求得;
(2)有(1)中所设Ak表示数学组评上k人(k=0,1,2),设Bi表示语文组评上i人(i=0,1,2)且每个事件之间为相互独立事件,又此问根据题意正面所包含的事件太多,利用正难则反的原则,可以根据对立事件来求解即可;
(3)利用随机变量的定义及随机变量的期望的定义即可求值.
(2)有(1)中所设Ak表示数学组评上k人(k=0,1,2),设Bi表示语文组评上i人(i=0,1,2)且每个事件之间为相互独立事件,又此问根据题意正面所包含的事件太多,利用正难则反的原则,可以根据对立事件来求解即可;
(3)利用随机变量的定义及随机变量的期望的定义即可求值.
解答:解:设Ak表示数学组评上k人(k=0,1,2),设Bi表示语文组评上i人(i=0,1,2).P(Ak)=
(
)k(
)2-k,P(Bi)=
(
)i(
)2-i=
(
)2.
(1)P=P(A1•B1)=P(A1)•P(B1)=
(
)(
)
(
)2=
;
(2)P=1-P(A0•B0)=1-P(A0)•P(B0)=1-(
)2(
)2=
;
(3)由题意ξ~B(2,
)
∴期望Eξ=2×
=
,方差Dξ=2×
×
=
,
答:(1)这两个组各有1人评上的概率是
;
(2)这两个组至少有1人评上的概率是
;
(3)数学组评上的人数ξ的期望Eξ=2×
=
,方差Dξ=2×
×
=
.
| C | k 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | i 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | i 2 |
| 1 |
| 2 |
(1)P=P(A1•B1)=P(A1)•P(B1)=
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 1 2 |
| 1 |
| 2 |
| 2 |
| 9 |
(2)P=1-P(A0•B0)=1-P(A0)•P(B0)=1-(
| 1 |
| 3 |
| 1 |
| 2 |
| 35 |
| 36 |
(3)由题意ξ~B(2,
| 2 |
| 3 |
∴期望Eξ=2×
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
答:(1)这两个组各有1人评上的概率是
| 2 |
| 9 |
(2)这两个组至少有1人评上的概率是
| 35 |
| 36 |
(3)数学组评上的人数ξ的期望Eξ=2×
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
点评:此题考查了随机变量的定义及离散型随机变量的期望,还考查了独立事件同时发生的定义及其概率公式及学生的理解题意的能力.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 和
和 ,且每个人是否评上互不影响.
,且每个人是否评上互不影响.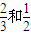 ,且每个人是否评上互不影响.
,且每个人是否评上互不影响.