题目内容

设椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）以F1、F2为左、右焦点，离心率e=
1
2
，一个短轴的端点（0，
3
）；抛物线C2：y2=4mx（m＞0），焦点为F2，椭圆C1与抛物线C2的一个交点为P．
（1）求椭圆C1与抛物线C2的方程；
（2）直线l经过椭圆C1的右焦点F2与抛物线C2交于A1，A2两点，如果弦长|A1A2|等于△PF1F2的周长，求直线l的斜率．
分析：（1）由离心率、短轴的端点坐标、及a2=b2+c2求得a，b的值，求得椭圆的方程．由抛物线的焦点坐标求得m的值，进一步得到抛物线方程；
（2）由于△PF1F2周长为 2a+2c=6，故弦长|A1A2|=6，用点斜式设出直线L的方程，代入抛物线方程化简，得到根与系数的关系，代入弦长公式求出斜率k的值．
解答：解：（1）由椭圆的离心率e=
c
a
=
1
2
，得
c2
a2
=
a2-b2
a2
=
1
4
，∴a2=
4
3
b2．
又b=
3
，∴a2=4，则a=2，c=1．
∴椭圆C1的方程为：
x2
4
+
y2
3
=1．
抛物线C2的焦点为（1，0），∴m=1，则抛物线方程为：y2=4x；
（2）由于△PF1F2周长为 2a+2c=6，故弦长|A1A2|=6，
设直线l的斜率为k，则直线l的方程为 y-0=k（x-1），
代入抛物线C2：y2=4x，化简得 k2x2-（2k2+4）x+k2=0，
∴x1+x2=
2k2+4
k2
，x1x2=1，
∴|A1A2|=
1+k2
•
(x1+x2)2-4x1x2

=
(1+k2)[(
2k2+4
k2
)2-4]
=6，解得：k=±
2
．
故直线l的斜率为：±
2
．
点评：本题考查了椭圆的标准方程及抛物线的标准方程求法，考查了直线与圆锥曲线的位置关系，训练了设而不求的解题思想方法和数学转化思想方法，考查了学生的计算能力，是高考试卷中的压轴题．
练习册系列答案
相关题目
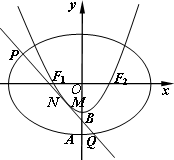精英家教网设椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：y=x2-1与y轴的交点为B，且经过F1，F2点．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）设M（0，-
4
5
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求△MPQ面积的最大值．
设椭圆 C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个顶点与抛物线 C2：x2=4
3
y 的焦点重合，F1，F2分别是椭圆的左、右焦点，离心率 e=
1
2
，过椭圆右焦点 F2的直线 l 与椭圆 C 交于 M，N 两点．
（1）求椭圆C的方程；
（2）是否存在直线 l，使得 
OM
•
ON
=-2，若存在，求出直线 l 的方程；若不存在，说明理由．
（2013•浦东新区二模）（1）设椭圆C1：
x2
a2
+
y2
b2
=1与双曲线C2：9x2-
9y2
8
=1有相同的焦点F1、F2，M是椭圆C1与双曲线C2的公共点，且△MF1F2的周长为6，求椭圆C1的方程；
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．
（2）如图，已知“盾圆D”的方程为y2=
4x            (0≤x≤3)
-12(x-4)  (3＜x≤4)
．设“盾圆D”上的任意一点M到F（1，0）的距离为d1，M到直线l：x=3的距离为d2，求证：d1+d2为定值； 
（3）由抛物线弧E1：y2=4x（0≤x≤
2
3
）与第（1）小题椭圆弧E2：
x2
a2
+
y2
b2
=1（
2
3
≤x≤a）所合成的封闭曲线为“盾圆E”．设过点F（1，0）的直线与“盾圆E”交于A、B两点，|FA|=r1，|FB|=r2且∠AFx=α（0≤α≤π），试用cosα表示r1；并求
r1
r2
的取值范围．
（2012•德州一模）设椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的一个顶点与抛物线C2：x2=4
2
y的焦点重合，F1、F2分别是椭圆的左、右焦点，离心率e=
3
3
，过椭圆右焦点F2的直线l与椭圆C交于M、N两点．
（I）求椭圆C的方程；
（Ⅱ）是否存在直线l，使得
OM
•
ON
=-1，若存在，求出直线l的方程；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网