题目内容
设f(x)＝lg
，则f(
)＋f(
)的定义域为
[ ]
A．
(－4，0)∪(0，4)
B．
(－4，－1)∪(1，4)
C．
(－2，－1)∪(1，2)
D．
(－4，－2)∪(2，4)
答案：B
解析：
解析：
|
本题是已知f(x)的定义域，而求函数f[g(x)]定义域的题型，则应首先求出函数f(x)＝lg 要使函数f(x)＝lg 即函数f(x)＝lg2＋ 所以要使函数f( 解①，得－4＜x＜4， 解②，原不等式可化为－x2＜x＜x2，即 解得x＜－1或x＞1， 故原不等式的解集为－4＜x＜－1或1＜x＜4， 即原函数的值域为(－4，－1)∪(1，4)． |
的定义域，再求f(
)＋f(
)的定义域．
或
解得－2＜x＜2，
练习册系列答案
相关题目
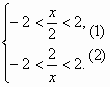
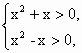
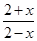，则f(
)＋f(
)的定义域为________．
，则f(
)＋f(
)的定义域为________．
，则f
＋f 
的定义域为( )
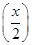，则f 
＋f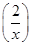 
的定义域为 ( )