题目内容
已知:命题q:集合A={x|x2+ax+1=0,x∈R},B={x|x>0},且A∩B=∅.(I)若命题q为真命题,求实数a的取值范围;
(II)若命题p:
 ,且|f(a)|<2,试求实数a的取值范围,使得命题p,q有且只有一个为真命题.
,且|f(a)|<2,试求实数a的取值范围,使得命题p,q有且只有一个为真命题.
【答案】分析:(I)对两集合交集为空集要有充分的认识,要注意考虑一个集合为空集的情况.要有分类讨论意识,准确将A∩B=φ进行合理转化是解决本题的关键.结合集合B可知,集合A=φ或者A⊆(-∞,0】.
(II)在第(I)问a的范围之下,求解出命题q成立的a的范围,然后依据p真q假、p假q真分别得出关于实数a的不等式组,从而求解出实数a的取值范围.
解答:解:(Ⅰ)因为A∩B=∅,故集合A应分为A=∅和A≠∅两种情况
(1)A=∅时,△=a2-4<0⇒-2<a<2;
(2)A≠∅时, ,所以A∩B=∅得a>-2,
,所以A∩B=∅得a>-2,
故实数a的取值范围为a>-2;
(Ⅱ)由|f(a)|<2得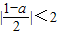 ,解得-3<a<5,若p真q假,则有
,解得-3<a<5,若p真q假,则有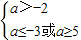 ,则a≥5;
,则a≥5;
若p假q真,则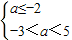 ,即-3<a≤-2,
,即-3<a≤-2,
故实数a的取值范围为-3<a≤-2或a≥5.
点评:本题主要考查了集合交集的定义,分类讨论思想和等价转化思想.将方程的根的问题进行适当的转化,列出不等式是解决本题的关键.正确求解含绝对值的不等式,对命题p,q有且只有一个为真命题进行合适转化也是正确求解本题所必需的.
(II)在第(I)问a的范围之下,求解出命题q成立的a的范围,然后依据p真q假、p假q真分别得出关于实数a的不等式组,从而求解出实数a的取值范围.
解答:解:(Ⅰ)因为A∩B=∅,故集合A应分为A=∅和A≠∅两种情况
(1)A=∅时,△=a2-4<0⇒-2<a<2;
(2)A≠∅时,
 ,所以A∩B=∅得a>-2,
,所以A∩B=∅得a>-2,故实数a的取值范围为a>-2;
(Ⅱ)由|f(a)|<2得
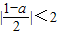 ,解得-3<a<5,若p真q假,则有
,解得-3<a<5,若p真q假,则有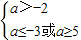 ,则a≥5;
,则a≥5;若p假q真,则
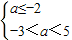 ,即-3<a≤-2,
,即-3<a≤-2,故实数a的取值范围为-3<a≤-2或a≥5.
点评:本题主要考查了集合交集的定义,分类讨论思想和等价转化思想.将方程的根的问题进行适当的转化,列出不等式是解决本题的关键.正确求解含绝对值的不等式,对命题p,q有且只有一个为真命题进行合适转化也是正确求解本题所必需的.

练习册系列答案
相关题目
 ,且|f(a)|<2,试求实数a的取值范围,使得命题p,q有且只有一个为真命题.
,且|f(a)|<2,试求实数a的取值范围,使得命题p,q有且只有一个为真命题. ,且|f(a)|<2,试求实数a的取值范围,使得命题p,q有且只有一个为真命题.
,且|f(a)|<2,试求实数a的取值范围,使得命题p,q有且只有一个为真命题.