题目内容
（2006•丰台区一模）设函数f(x)=sin(ωx+| π |
| 4 |
（Ⅰ）求f（x）的表达式；
（Ⅱ）若f(x)•sin(
| π |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
| π |
| 2 |
分析：（Ⅰ）由函数图象可得
=
-
=
，从而可求T，由T=
可求得ω，于是可得f （x）的表达式；
（Ⅱ）由正余弦的诱导公式及倍角公式可将f(x)•sin(
-2x)=
，x∈(
，
)转化为：cos4x=
，结合条件x∈（
，
），得到4x∈（π，2π），从而可求得x=
=
+
，再利用两角和的正切即可求得tanx的值．
| T |
| 4 |
| 3π |
| 8 |
| π |
| 8 |
| π |
| 4 |
| 2π |
| ω |
（Ⅱ）由正余弦的诱导公式及倍角公式可将f(x)•sin(
| π |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 4 |
| π |
| 3 |
解答：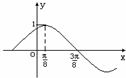
解：（Ⅰ）设f（x）=sin（ωx+
）的周期为T，
∵
=
-
=
，
∴T=π，又T=
，
∴ω=2，
所以 f(x)=sin(2x+
)…（3分）
（Ⅱ）∵f(x)•sin(
-2x)=sin(2x+
)sin(
-2x)=sin(2x+
)cos(2x+
)=
，
∴sin（4x+
）=
，即cos4x=
，
又x∈（
，
），
∴4x∈（π，2π），
∴4x=
，x=
…（9分）
∴tanx=tan
=tan(
+
)=
=
=2+
…（13分）
解：（Ⅰ）设f（x）=sin（ωx+| π |
| 4 |
∵
| T |
| 4 |
| 3π |
| 8 |
| π |
| 8 |
| π |
| 4 |
∴T=π，又T=
| 2π |
| ω |
∴ω=2，
所以 f(x)=sin(2x+
| π |
| 4 |
（Ⅱ）∵f(x)•sin(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 4 |
∴sin（4x+
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又x∈（
| π |
| 4 |
| π |
| 2 |
∴4x∈（π，2π），
∴4x=
| 5π |
| 3 |
| 5π |
| 12 |
∴tanx=tan
| 5π |
| 12 |
| π |
| 4 |
| π |
| 6 |
tan
| ||||
1-tan
|
1+
| ||||
1-
|
| 3 |
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式及三角函数的恒等变换及化简求值，难点在于得到cos4x=
，结合条件求得x=
，着重考查三角函数公式的灵活运用能力，属于中档题．
| 1 |
| 2 |
| 5π |
| 12 |
练习册系列答案
阅读快车系列答案
相关题目